Курсовая работа: Постановка и решение транспортной параметрической задачи

4.3 Решение задачи аналитическим методом

Полагая k=0, по известному алгоритму составим опорное решение методом Фогеля. Полученный опорный план перевозок и алгоритм выполнения с нахождением минимальных разностей стоимостей перевозок (C_ij ) в каждом столбце и строке изображен на рисунке 4.3.1.

Рис. 4.3.1. Составление первого опорного решения задачи по методу Фогеля

Процесс выполнения получения опорного решения с последовательным назначением перевозок в ячейки: А₄ В₃ - А₃ В₃ - А₃ В₁ - А₁ В₁ - А₁ В₂ - A₂ B₂ .

Проверка плана на вырожденность: m+n-1=6. План невырожденный.

Проверим опорное решение на оптимальность по методу потенциалов. Расчет потенциалов строк и столбцов для занятых из условия v_i + u_j = c_ij для занятых клеток и проверка условия v_i + u_j ≤ c_ij для незанятых приведены в таблице 4.3.1.

Решение, полученное при k=0, является оптимальным для всех значений параметра k, удовлетворяющих условию .

Из условия для свободных клеток найдем:

∆₁₃ = v₃ + u₁ - c'₁₃ = -1 + 2 - 2 = -1

∆₂₁ = v₁ + u₂ - c'₂₁ = 0 + 3 - 5 = -2

∆₂₃ = v₃ + u₂ - c'₂₃ = -1 + 3 - 6 = -4

∆₃₂ = v₂ + u₃ - c'₃₂ = 2 + 4 - 7 = -1

∆₄₁ = v₁ + u₄ - c'₄₁ = 0 + 2+k - 6 = -4 + k

∆₄₂ = v₂ + u₄ - c'₄₂ = 2 + 2+k - 8 = -4 + k

Табл. 4.3.1. Проверка первого опорного решения на оптимальность методом потенциалов

заполненные			незаполненные
№	vi + uj = cij	значения	№	vi + uj ≤ cij	условие
А1 В1	v1 +u1 =2	v1 =0, u1 =2	А1 В3	v3 +u1 <=2	соблюдается
А1 В2	v2 +u1 =4	v2 =2	А2 В1	v1 +u2 <=5	соблюдается
A2 B2	v2 +u2 =5	u2 =3	А2 В3	v3 +u2 <=6	соблюдается
A3 B1	v1 +u3 =4	u3 =4	А3 В2	v2 +u3 <=7	соблюдается
A3 B3	v3 +u3 =3	v3 = -1	A4 B1	v1 +u4 <=6	соблюдается
A4 B3	v3 +u4 =1+k	u4 =2+k	A4 B2	v2 +u4 <=8	соблюдается

Определение значений k₁ и k₂ :

k₁ = max(-a_ij /B_ij ) = т.к. все B_ij ≥ 0

k₂ = min(-a_ij /B_ij ) = (-a₄₁ /B₄₁ ; -a₄₂ /B₄₂ ) = min(4;4) = 4. Все B_ij > 0.

Так как по условию задачи k≥0, то оптимальное решение сохраняется при 0≥k≥4.

При этом минимальная стоимость транспортных расходов составляет:

F(X₁ )_min = 20*(1+k) + 40*3 + 30*4 + 90*2 + 10*4 + 70*5 = 830 + 20k

Таким образом, при , F(X₁ )_min = 830 + 20k и

.

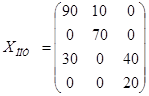Чтобы получить оптимальное решение при k≥4 перераспределим поставки товаров в клетку (4,1), где k₂ =4. Вновь полученное распределение с учетом изменения стоимости перевозки в ячейке A₄ B₃ (k=4) представлено на рисунке 4.3.2.

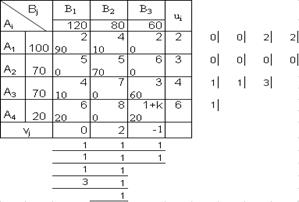
Рис. 4.3.2. Составление второго опорного решения задачи по методу Фогеля

Процесс выполнения получения опорного решения с последовательным назначением перевозок в ячейки: А₄ В₁ - А₃ В₃ - А₃ В₁ - А₁ В₁ - А₁ В₂ - A₂ B₂ .

Проверка плана на вырожденность: m+n-1=6. План невырожденный.