Курсовая работа: Постановка и решение транспортной параметрической задачи
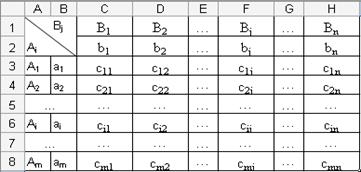
Рис. 3.1. Фрагмент окна программы MsExcel: Модель таблицы «Стоимость перевозок».
2. В таблице «Стоимость перевозок» в ячейках запасов поставщиков и потребностей потребителей записать количество запасов поставщиков и потребностей потребителей соответственно, указанное в условии задачи.
3. Таблицу "План перевозок" создать с пустыми полями (заполненными единицами), заранее заданного числового формата. В ячейках запасов (потребностей) каждого поставщика (потребителя) ввести формулу, выполняющую суммирование всех возможных поставок этого поставщика (потребителя).
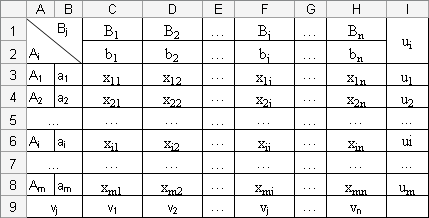
Рис. 3.2. Фрагмент окна программы MsExcel: Модель таблицы «План перевозок».
4. В ячейке целевой функции ввести формулу, высчитывающую сумму произведений элементов матрицы "Стоимость перевозок" и соответствующих элементов матрицы "План перевозок".
5. В диалоговом окне функции "Поиск решения" установить необходимые ограничения, в целевой ячейке указать адрес ячейки с формулой целевой функции и установить ее равной минимальному значению, в качестве изменяемых ячеек выбрать диапазон всех элементов матрицы "План перевозок". Ограничения в "Поиске решений" заключаются в необходимости равенства запасов (потребностей), в матрице "План перевозок" соответствующим запасам и потребностям, указанным в матрице "Стоимость перевозок". Также все элементы матрицы "План перевозок" должны быть неотрицательными и целочисленными.
6. В диалоговом окне "Параметры поиска решения" установить параметр "Линейная модель" и число итераций, равное 100.
7. Выполнить функцию "Поиск решения" нажатием на кнопку "Выполнить". В качестве отчета по результатам выбрать необходимый пункт в списке "Тип отчета" диалогового окна «Результаты поиска решения».
После выполнения вышеуказанных действий при условии, что задача имеет решение, в матрице «План перевозок» запишется оптимальное решение задачи, т.е. оптимальный план перевозок с указанием объемов поставок в каждой ячейке. В ячейке с целевой функцией запишутся совокупные затраты поставок.
4. Решение параметрической транспортной задачи
4.1 Постановка параметрической транспортной задачи
Имеется четыре поставщика однородного груза с объемами поставок 100, 70, 70, 20 т. и три потребителя с объемами потребления 120, 80, 60 т. Стоимость транспортных расходов задана матрицей
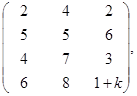
причем стоимость перевозки груза от четвертого поставщика до третьего потребителя изменяется в диапазоне 0≤k≤9.
Определить оптимальный план перевозок, обеспечивающий минимальные транспортные расходы.
Изобразим матричную запись задачи (табл. 4.1.1)
Табл. 4.1.1. Матричная запись задачи
|
Bj Ai | B1 | B2 | B3 | |
| 120 | 80 | 60 | ||
| A1 | 100 | 2 | 4 | 2 |
| X11 | X12 | X13 | ||
| A2 | 70 | 5 | 5 | 6 |
| X21 | X22 | X23 | ||
| A3 | 70 | 4 | 7 | 3 |
| X31 | X32 | X33 | ||
| A4 | 20 | 6 | 8 | 1+k |
| X41 | X42 | X43 | ||
4.2 Математическая модель задачи
Целевая функция
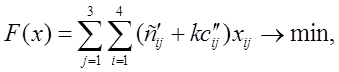 .
.
где Xij – объем поставок груза,
при ограничениях:
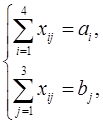
Xij ≥0, ![]()
![]()
Подробные ограничения по потребностям и запасам каждого потребителя и поставщика соответственно отражены в Таблице 4.2.1.