Для повышения точности системы в установившихся режимах можно повысить порядок астатизма системы, для чего необходимо передаточную функцию разомкнутой системы (1.1) разделить на оператор Лапласа:

По ЛАЧХ и ЛФЧХ разомкнутой системы (рисунок 1.3) можно сказать, что система в замкнутом состоянии будет устойчива. Тогда рассчитаем аналитически ошибки системы в типовых режимах:2.5

- ошибка по положению равна ;

- ошибка по скорости 1 / 24 =0,042

- ошибка по ускорению равна .

Эти значения соответствуют результатам построения переходных процессов (рисунок 1.4).

Рисунок 1.3 – Логарифмические частотные характеристики разомкнутой системы с астатизмом 1-го порядка

а)

б)

в)

а) переходная функция;

б) реакция на линейно нарастающий сигнал;

в) реакция на сигнал, увеличивающийся с постоянным ускорением

Рисунок 1.4 – Реакция системы с астатизмом 1-го порядка на типовые входные воздействия

1.3 Исследование системы с астатизмом второго порядка

При увеличении порядка астатизма системы до второй степени система становится неустойчивой (рисунок 1.5), поэтому нет смысла рассматривать точность системы в установившихся режимах.

Анализируя влияние астатизма системы на точность и устойчивость, можно сделать следующие выводы:

Рисунок 1.5 – Логарифмические частотные характеристики разомкнутой системы с астатизмом 2-го порядка

2 Коррекция путем изменения коэффициента усиления системы

2.1 Исследование влияние величины коэффициента усиления разомкнутой системы на запасы устойчивости

В соответствии с индивидуальным заданием пронаблюдаем за влиянием коэффициента усиления системы пропорционального регулятора на устойчивость, точность и качество системы автоматического управления.

Передаточная функция объекта управления:

. (2.1)

Распределение нулей и полюсов замкнутой системы и частотные характеристики разомкнутой системы (рисунок 2.1) говорят о неустойчивости замкнутой системы при единичном коэффициенте усиления пропорционального регулятора.

Рисунок 2.1 - Распределение нулей и полюсов замкнутой системы и частотные характеристики разомкнутой системы

Для наблюдения влияния величины пропорционального регулятора на устойчивость, точность и качество системы автоматического управления создадим M-file со следующим программным кодом:

Анализируя логарифмические частотные характеристики разомкнутой системы (рисунок 2.2), можно сказать, что при увеличении коэффициента усиления системы ЛАЧХ смещается вверх, при этом увеличивается частота среза, следовательно, запасы устойчивости по амплитуде и по фазе уменьшаются.

Рисунок 2.2 - Логарифмические частотные характеристики разомкнутой системы при изменении коэффициента усиления регулятора

2.2 Исследование зависимости ошибки в установившихся режимах от коэффициента усиления системы

Из рисунка 1.2 видно, что из пяти выбранных устойчивыми являются только первые две системы с коэффициентами усиления регуляторов и . Проанализируем качество систем с этими регуляторами. Для этого дополним M-file следующим программным кодом :

Аналитический расчет ошибок системы в типовых режимах дает следующие результаты:

система с :

- ошибка по положению равна ;

- ошибка по скорости ;

- ошибка по ускорению равна ;

система с :

- ошибка по положению равна ;

- ошибка по скорости ;

- ошибка по ускорению равна .

Анализируя полученные результаты и графики переходных процессов (рисунок 2.3), можно сделать следующие выводы: при увеличении (уменьшении) коэффициента усиления системы ее устойчивость уменьшается (увеличивается), увеличивается (уменьшается) перерегулирование, колебательность и время переходного процесса, возрастает (снижается) быстродействие, точность системы повышается (понижается).

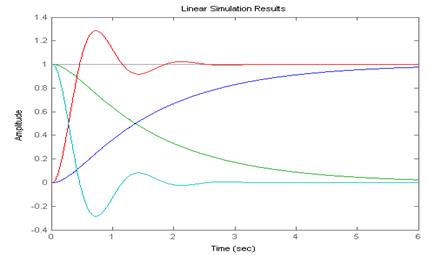
a)

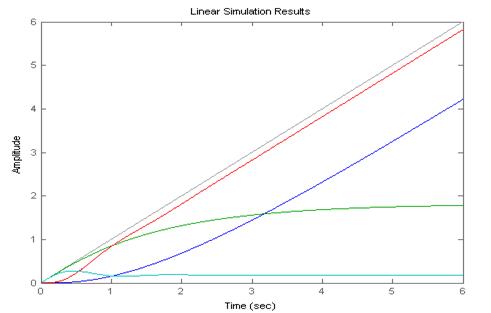
б)

а) переходная функция;