Курсовая работа: Повышение точности и устойчивости системы автоматического управления

- максимальная ошибка слежения при задающем воздействии, максимальная скорость и ускорение изменения которой и ;

- время регулирования ;

- перерегулирование .

В связи с ужесточившимися по сравнению с пунктом 2 требованиями к качеству регулирования применением пропорционального регулятора невозможно добиться устойчивости и одновременной точности системы автоматического регулирования. Для коррекции объекта управления (2.1) в данном случае следует применить интегрирующее корректирующее устройство, имеющее передаточную функцию:

.

Причем .

3.2 Аналитическое определение параметров регулятора

Для настройки параметров регулятора воспользуемся методикой, представленной в [2, с. 338 - 342]:

1. Дополним передаточную функцию объекта коэффициентом , удовлетворяющим требования к системе в области низких частот:

.

Следовательно,

.

2. Определим частоту, на которой .

Из логарифмических частотных характеристик разомкнутой системы (рисунок 3.1) видно, что система обладает запаздыванием по фазе на частоте .

3. Зададим значение нуля регулятора:

4. Определим значение полюса регулятора:

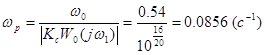
5. В результате передаточная функция регулятора примет вид:

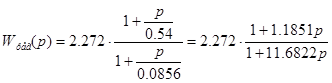(3.1)

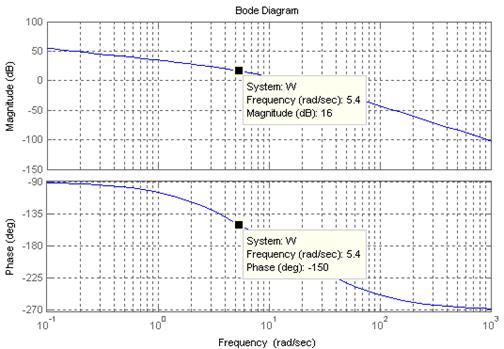
Рисунок 3.1 – Логарифмические частотные характеристики разомкнутой системы

ЛЧХ скорректированной системы (рисунок 3.2) говорят о том, что с помощью синтезированного корректирующего устройства удалось добиться приемлемых (по крайней мере близких к требуемым) показателей качества системы. Однако регулятор еще требует «подгонки».

Для построения регулятора с отставанием по фазе удобно воспользоваться следующим программным кодом:

Рисунок 3.2 – Логарифмические частотные характеристики скорректированной системы

3.3 Определение параметров регулятора с помощью среды Control System Toolbox

Более профессиональный подход к синтезу интегрирующего корректирующего устройства может быть осуществлен при помощи MATLAB Control System Toolbox. Для этого запускаем функцию sisotool(«объект управления») и создаем запретные зоны (рисунок 3.3):

Рисунок 3.3 – Запретные зоны на логарифмических частотных характеристиках объекта управления и корневом годографе

Анализ рисунка 3.3 позволяет сказать о неустойчивости замкнутой системы и наметить пути дальнейшей коррекции системы:

- необходимо добавить регулятор интегрирующего типа (полюс и ноль корректирующего устройства);

- можно уменьшить коэффициент усиления, приблизив ЛАЧХ к запретной зоне.

Изменяя величины нуля, полюса и коэффициента усиления регулятора, добиваемся требуемых показателей качества (рисунки 3.4 и 3.5). Передаточная функция регулятора (рисунок 3.6) имеет следующий вид:

Сравнение результатов (3.1) и (3.2) говорит о схожести регуляторов, и выбор его конкретной конфигурации лежит в области инженерного творчества и должен опираться на соображения целесообразности, простоты реализации и минимизации стоимости.

Рисунок 3.4 – Частотные характеристики и корневой годограф скорректированной системы управления

Рисунок 3.5 – Переходная функция скорректированной системы

Рисунок 3.6 – Частотные характеристики объекта управления, регулятора и скорректированной системы

Экспортируем ПФ регулятора в рабочую область MATLABа и определим ошибку системы при типовых воздействиях (рисунок 3.7):

а)

б)

в)