Курсовая работа: Практическое применение интерполирования гладких функций
где постоянная А находится из условия fj (xj )=1, тогда

Таким образом, получаем, что
fj (x)![]()
Получаем, что поставленную задачу решает многочлен
(8) 
Многочлен (8) называется интерполяционным многочленом Лагранжа.
Задача 1.
Пусть задана интерполяционная таблица:
| i | 0 | 1 | 2 | 3 |
| 0 | 2 | 3 | 5 | |
| 1 | 3 | 2 | 5 |
Построить интерполяционный полином Лагранжа.
Решение. Из (8) следует:

Задача 2.
Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой, проходящей через точки Р0 (х0 , у0 ) и Р1 (х1 , у1 ), если х0 =-1, у0 =-3, х1 =2, у1 =4.
Решение. В данном случае многочлен Лагранжа примет вид
 .
.
Уравнение искомой прямой есть ![]() .
.
1.5 Про погрешность полинома
По строению ![]() (
(![]() ). Но, в общем, это не так и
). Но, в общем, это не так и ![]() (
(![]() ,
,![]() ), так как интерполирование предполагает приближенное нахождение:
), так как интерполирование предполагает приближенное нахождение:
![]() (
(![]() )
)
И в связи с этим необходимо говорить о погрешности интерполирования. Заранее сказав, ![]() разность этого выражения нужно найти.
разность этого выражения нужно найти.
Замечание 1 .
![]() (
(![]() )
)
чем постоянно записывать равенство, слагаемое ![]() называют остаточным членом (или погрешность интерполяции).
называют остаточным членом (или погрешность интерполяции).
Теорема 1.
Если ![]() [a,b] [2]
[a,b] [2]
(9) 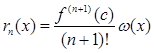 (
(![]() ,
,![]() ), где
), где ![]()
![]() [a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций.
[a,b] в промежутке беспрерывно n+1 раз объясняет совокупность дифференцируемых функций.