Курсовая работа: Практическое применение интерполирования гладких функций
Пусть 
. По (19) получим 
в последовательной форме используем метод интегрирования по частям, и изменяем его:
Отсюда выходит следующее неравенство:
(20) 
называют формулой Тейлора с остаточным членом в интегральной форме.
Возьмем некоторую функцию 
, чтобы равенство (18) было правильным 
. При рассмотрении второго слагаемого полинома, достаточно показать что Î С( m) .
При изучении производной 
полезно использовать дифференцирование интеграла, зависящего от параметра. Эта формула в математическом анализе очень известна и определяет следующее:
(21) 
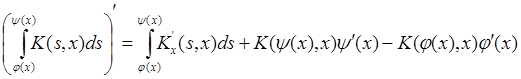
здесь 
вдобавок 
Таким образом, находим в нашем случае необходимый вид:
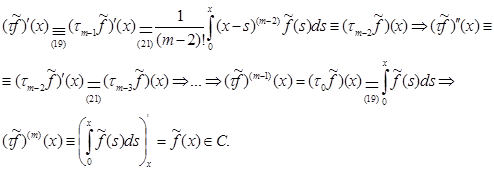
Значит 
.
Замечание 6.
Рассмотрев, оператор 
из последнего размышления вытекает полезное рассуждение:
(22) 
Заключение
Мы убедились, что в вычислительной математике существенную роль играет интерполяция функций, значения которой совпадают со значениями заданной функции в некотором числе точек.
В данной курсовой работе рассматривается интерполирование функции полиномами, непосредственно непрерывных функций на отрезке и в точке, определили понятие погрешности интерполяции.
У нас возникла задача о восстановлении непрерывной функции по ее табличным значениям, поэтому в данной работе были приведены конкретные примеры по построению интерполяционного полинома Лагранжа, по оцениванию погрешности интерполяционного полинома.
В нашем случае для более полного раскрытия данной темы подробно проиллюстрировано само понятие интерполяции, далее интерполирование непосредственно гладкой функции и интерполирование гладкой функции в точке.
Список использованной литературы
1. Н.С.Габбасов. Некоторые применения производной. Наб.Челны, 1998г.
2. Я.С.Бугров, С.М.Никольский. Дифференциальное и интегральное исчисление. М.: «Наука», 1984г.
3. С.М.Никольский. Курс математического анализа. М.: «Наука», 1990г.
4. Л.Д.Кудрявцев. Краткий курс математического анализа. М.: «Наука», 1989г.
5. И.А.Марон. Дифференциальное и интегральное исчисление. М.: «Наука», 1970г.
6. А.А.Самарский. Введение в численные методы. М.: «Наука», 1987.
[1] Здесь Hn – это множество всех алгебраических многочленов степени n.
[2] На непрерывном отрезке и в точке 
обозначили множество функции, имеющей производную по Тейлору m-го порядка.
(естественно, 