Курсовая работа: Предельные точки

Содержание:

Введение

1. Эквивалентные множества. Счетные и несчетные множества. Мощность континуума

2. Замкнутые и открытые множества

3. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве

Заключение

Используемая литература

Введение

Начинать курсовую работу по этой теме, на мой взгляд, стоит с определения понятия множество, так как оно является одним из основных понятий математического анализа.

Множество − это совокупность объектов любой природы. Определение множества есть описательное определение с помощью слов разговорного языка.

Объекты, образующие в своей совокупности данное множество, называются его элементами или точками. Для обозначения различных множеств чаще всего используются заглавные (прописные) буквы латинского алфавита, а для обозначения элементов этих множеств – малые (строчные) буквы.

Два множества называются равными, если они состоят из одних и тех же элементов. Это записывают так: или .

Если элемент a принадлежит множеству А, то пишут: , если же не принадлежит, то записывают так: .

Если все элементы множества принадлежат множеству , то называется подмножеством множества , и пишут: .

Очевидно, что если и , то .

Обычно, удобнее рассматривать все множества, участвующие в каком-либо рассуждении, как подмножества некоторого фиксированного множества , которое называют универсальным.

Для того чтобы с определенностью говорить о каком-либо множестве , нужен четкий критерий, правило, условие, свойство, которое дает возможность установить, какие именно элементы входят в . Если обозначить это условие через , то тот факт, что условие порождает множество , записывают следующим образом: .

Может оказаться так, что для некоторого свойства во всем множестве вообще нет элементов, которые удовлетворяют данному условию. В таком случае говорят, что это пустое множество, оно не содержит ни одного элемента.

Для краткости вместо некоторых часто употребляемых выражений общепринято использовать особые математические знаки, называемые кванторами:

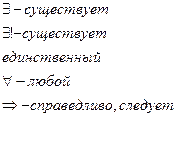
Множество называется объединением (или суммой) множеств и ,если оно состоит из тех и только тех элементов, которые принадлежат хотя бы одному из указанных множеств.

Обозначается это так:

.

Свойства:

.

Пересечением множеств и называется множество , состоящее из всех элементов, принадлежащих одновременно и , и , т.е. элементов, общих для этих множеств. Доказать равенство двух множеств - это значит доказать, что всякий элемент , принадлежащих правой части равенства, принадлежит и левой, и наоборот.

Для произвольной совокупности множеств , где пробегает все элементы некоторого множества , пишут

,

если есть объединение всех множеств

--> ЧИТАТЬ ПОЛНОСТЬЮ <--