Курсовая работа: Приложение интегрального и дифференциального исчисления к решению прикладных задач
2.функция кусочно-монотонна на сегменте [a, b].
Теорема Дирикле: Пусть периодическая функция f (x) с периодом 2π удовлетворяет на любом сегменте условиям Дирикле. В таком случае ряд Фурье, соответствующий этой функции, сходится во всех точках числовой оси. При этом в каждой точке непрерывности функции f (x) сумма ряда S (x) равна значению функции в этой точке. В каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x→x0 слева и справа, т.е.:
S(x) = 0,5[f(x0 + 0)+f(x0 - 0)]
Во всех точках непрерывности функции f(x) ряд сходится к значениям функции в этих точках, т.е. S(x)=f(x) на интервале [0,
; в точке x=0 (точка разрыва функции) ряд сходится к 0, т.к.
Ответ: S(0)=0
c) Нарисовать график суммы ряда на отрезке [-2;6] :
1) для четного
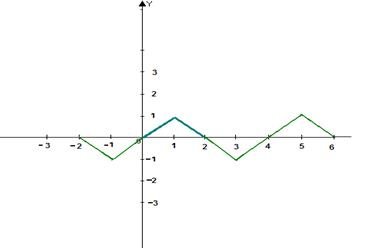
2) для нечетного
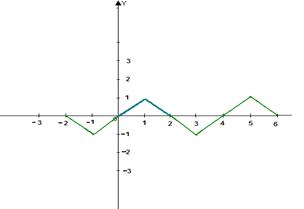
c) Пользуясь равенством Парсеваля, найти сумму:
Теория: Для функции f(x), такой, что f2 (x)ÎL(-p;p), справедливо равенство Парсеваля:
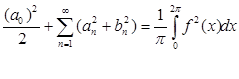
Решение: Период рассматриваемой функции равен p, поэтому поменяем пределы интегрирования с [0;2p] на [0;p], а коэффициент 2 вынесем, тогда:
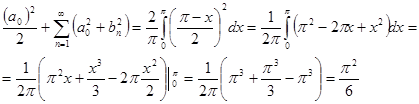
Ответ: 