Курсовая работа: Применение интегралов к решению прикладных задач
Вступление
Известно, какие замечательные и разнообразные приложения имеет математический анализ как в самой математике, так и в смежных областях знания. Поэтому сама мысль о связи математического анализа с другими математическими дисциплинами и с потребностями практики должна быть усвоена учащимися при изучении основ анализа уже в школе. Изложенный в данной работе материал лишь немногим связан со школьным курсом. В школе в 10-11 классах изучаются неопределённые и определённые интегралы, практикуется вычисление простейших интегралов и нахождение площади криволинейной трапеции, что составляет лишь малую часть всего интегрального исчисления.
интеграл площадь объем статический момент
1. Определённый интеграл
1.1 Площадь криволинейной трапеции
Вычислим площадь плоских фигур при помощи интегралов.
На первом месте рассмотрим в строгом изложении задачу об определении площади криволинейной трапеции ![]() (чертёж 1). Эта фигура ограничена сверху кривой
(чертёж 1). Эта фигура ограничена сверху кривой ![]() , имеющей уравнение
, имеющей уравнение ![]() , где
, где ![]() - положительная и непрерывная в промежутке
- положительная и непрерывная в промежутке ![]() функция; снизу она ограничена отрезком
функция; снизу она ограничена отрезком ![]() оси
оси ![]() , а с боков – двумя ординатами
, а с боков – двумя ординатами ![]() и
и ![]() (каждая из которых может свестись к точке).
(каждая из которых может свестись к точке).
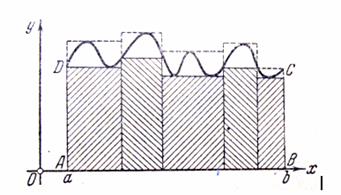
Чертёж 1.
Так как площадь P рассматриваемой фигуры ABCD существует, то будем вести речь лишь об её вычислении. С этой целью разобьём промежуток ![]() на части, вставив между a и b ряд точек
на части, вставив между a и b ряд точек ![]() . Обозначив через
. Обозначив через ![]() и
и ![]() , соответственно, наибольшее и наименьшее значения функции
, соответственно, наибольшее и наименьшее значения функции ![]() в i -м промежутке(i=0,1,…,n-1), составим суммы (Дарбу)
в i -м промежутке(i=0,1,…,n-1), составим суммы (Дарбу)
![]() ,
, ![]() .
.
Они, очевидно, представляют собой площади ступенчатых фигур, составленных, соответственно, из входящих и выходящих прямоугольников(см. чертёж). Поэтому ![]() . Но при стремлении к нулю наибольшей из разностей
. Но при стремлении к нулю наибольшей из разностей ![]() обе суммы имеют своим пределом интеграл
обе суммы имеют своим пределом интеграл 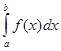 , следовательно, ему и равна искомая площадь P =
, следовательно, ему и равна искомая площадь P = 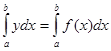 . (1)
. (1)
Если криволинейная трапеция CDFE ограничена и снизу и сверху кривыми (чертёж 2), уравнения которых ![]() и
и ![]()
![]() , то, рассматривая её как разность двух фигур
, то, рассматривая её как разность двух фигур ![]() и
и ![]() , получим площадь названной трапеции в виде P =
, получим площадь названной трапеции в виде P =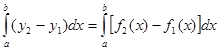 . (2)
. (2)
Пусть теперь дан сектор AOB (чертёж 3), ограниченной кривой AB и двумя радиусами-векторами AO и OB (каждый из которых может свестись к точке). При этом кривая AB задаётся полярным уравнением ![]() , где
, где ![]() - положительная непрерывная в промежутке
- положительная непрерывная в промежутке ![]() функция.
функция.
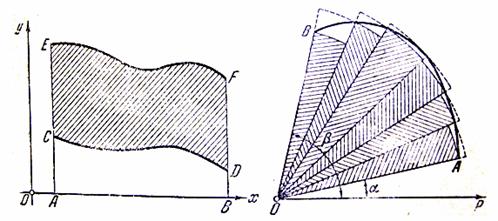
Чертёж 2. Чертёж 3.
Вставив между ![]() и
и ![]() (см. чертёж) значения
(см. чертёж) значения ![]() , проведём соответствующие этим углам радиус-векторы. Если ввести и здесь наименьшее и наибольшее значение функции
, проведём соответствующие этим углам радиус-векторы. Если ввести и здесь наименьшее и наибольшее значение функции ![]() в
в ![]() и
и ![]() , то круговые секторы, описанные этими радиусами, будут, соответственно, входящими и выходящими для фигуры(P ). Составим отдельно из выходящих секторов две фигуры, площади которых будут
, то круговые секторы, описанные этими радиусами, будут, соответственно, входящими и выходящими для фигуры(P ). Составим отдельно из выходящих секторов две фигуры, площади которых будут ![]() и
и ![]() .
.
В этих суммах ![]() и
и ![]() легко узнать суммы Дарбу для интеграла
легко узнать суммы Дарбу для интеграла  ; при стремлении к нулю наибольшей из разностей
; при стремлении к нулю наибольшей из разностей ![]() обе они имеют пределом этот интеграл. Тогда фигура (P ) квадрируема и P =
обе они имеют пределом этот интеграл. Тогда фигура (P ) квадрируема и P =  . (3)
. (3)
Примеры:
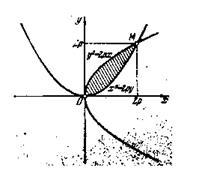
1). Определить площадь фигуры, заключённой между двумя конгруэнтными параболами ![]() и
и ![]() (чертёж 4).
(чертёж 4).
Очевидно, нужно воспользоваться формулой (2), полагая там ![]() ,
, ![]() . чертёж 4.
. чертёж 4.
Для установления промежутка интегрирования решим совместно данные уравнения и найдём абсциссу точки M пересечения обеих парабол, отличной от начала; она равна 2p . Имеем
 .
.
2). Формула (1) может быть использована и в том случае, если кривая, ограничивающая криволинейную трапецию, задана параметрически или уравнениями ![]() ,
, ![]() .
. ![]() . Произведя замену в интеграле (1), получим (в предположении, что
. Произведя замену в интеграле (1), получим (в предположении, что ![]() при
при ![]() и
и ![]() при
при ![]() ):
):  . (4)
. (4)
Если, например, при вычислении площади эллипса исходить из его параметрического представления ![]() ,
, ![]() и учесть, что
и учесть, что ![]() возрастает от
возрастает от ![]() до
до ![]() , когда
, когда ![]() убывает от
убывает от ![]() до нуля, то найдём
до нуля, то найдём  . Мы вычислили площадь верхней половины эллипса и удвоили её.
. Мы вычислили площадь верхней половины эллипса и удвоили её.

Чертёж 5.
