Курсовая работа: Применение интегралов к решению прикладных задач

1.4 Площадь поверхности вращения

Рассмотрим вопрос о вычислении площади поверхности вращения. Вычислим площадь поверхности вращения, считая её существующей и обладающей свойством аддитивности.

Пусть имеем на плоскости xy (именно в верхней полуплоскости) некоторую кривую AB , заданную уравнением вида , , , (10)

Где и - функции от параметра, непрерывные вместе со своими производными. Для простоты будем предполагать её незамкнутой и лишённой кратных точек. Нам удобно ввести в качестве параметра дугу s , отсчитываемую от точки , и перейти к представлению , , (11)

Параметр s изменяется здесь от 0 до S , если через S обозначить длину всей кривой AB .

Задача состоит в определении площади Q поверхности, полученной от вращения кривой AB вокруг осиx . Роль независимой переменной играет .

Если выделить элемент ds кривой (чертёж 12), то его приближённо можно принять за прямолинейный и вычислять соответствующий ему элемент площади как площадь усечённого конуса с образующей ds и радиусами основания y и y + dy . Тогда, по известной из школьного курса формуле, . Впрочем, это ещё не та формула, к которой мы стремимся – произведение двух бесконечно малых надо отбросить. Мы придём к линейной относительно формуле , откуда уже, «суммируя», окончательно получим 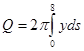(12)

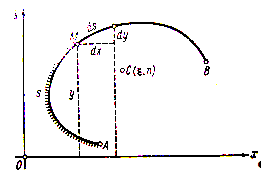
где под y надлежит разуметь фигурирующую в (11) функцию.

Если вернуться к общему параметрическому заданию (10) нашей кривой, то, произведя в предшествующем интеграле замену переменной, преобразуем его к виду (чертёж 12)

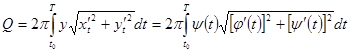. (12а)

В частности, если кривая задана явным уравнением , так что в роли параметра оказывается x , будем иметь:

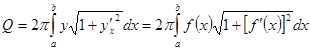. (12б)

Примеры:

1). Определить площадь поверхности шарового пояса.

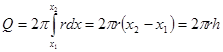Пусть полукруг, описанный около начала радиусом r , вращается вокруг оси x . Из уравнения круга имеем ; далее, , , . В таком случае площадь поверхности пояса, описанного дугой, концы которой имеют абсциссы и , по формуле (12б) будет , где h – высота пояса. Таким образом, площадь поверхности шарового пояса равна произведению окружности большого круга на высоту пояса. В частности, при и , т.е. при , получаем площадь всей шаровой поверхности .

2). Найти площадь поверхности, образованной вращением дуги циклоиды , .

Так как , , то

.

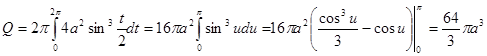1.5 Нахождение статических моментов и центра тяжести кривой

Как известно, статический момент K материальной точки массы m относительно некоторой оси равен произведению из массы m на расстояние d точки от оси. В случае системы n материальных точек с массами , лежащих в одной плоскости с осью, соответственно, на расстояниях от оси, статический момент выразится суммой .

При этом расстояния точек, лежащих по одну сторону от оси, берутся со знаком плюс, а расстояния точек по другую сторону – со знаком минус.

Если же массы не сосредоточены в отдельных точках, но расположены сплошным образом, заполняя линию или плоскую фигуру, то тогда для выражения статического момента вместо суммы потребуется интеграл.

Остановимся на определении статического момента относительно оси x масс, расположенных вдоль некоторой плоской кривой AB . При этом иы предположим кривую однородной, так что её линейная плотность (т.е. масса, приходящаяся на единицу длины) будет постоянной; для простоты допустим даже, что =1 (в противном случае полученный результат лишь умножить на ). При этих предположениях масса любой дуги нашей кривой измеряется просто её длиной, и понятие о статическом моменте приобретает чисто геометрический характер. Заметим, вообще, что когда говорят о статическом моменте (или центре тяжести) кривой – без упоминания о распределении вдоль по ней масс, то всегда имеют ввиду статический момент (центр тяжести), определённый именно при указанных предположениях.

Выделим снова некий элемент кривой (масса которого также выражается числом ). Приняв этот элемент приближённо за материальную точку, лежащую на расстоянии y от оси, для его статического момента получим выражение . Суммируя эти элементарные статические моменты, причём за независимую переменную возьмём дугу s , отсчитываемую от точки A , получим 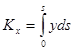. Аналогично выражается и момент относительно оси y : 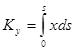. Конечно, здесь предполагается, что y (или x ) выражено через s . Практически в этих формулах выражают s через ту переменную t , x или , которая играет роль независимой в аналитическом представлении кривой.

Статические моменты и кривой позволяют легко установить положение от центра тяжести . Точка C обладает тем свойством, что если в ней сосредоточить всю «массу» S кривой (выражаемую тем же числом, что и длина), то момент этой массы относительно любой оси совпадает с моментом кривой относительно этой оси. В частности, если рассмотреть моменты кривой относительно осей координат, то найдём 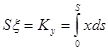, , 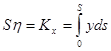откуда 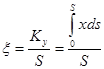, 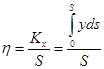. (13)

Из формулы для ординаты центра тяжести мы получаем замечательное геометрическое следствие. В самом деле, имеем , откуда . Но правая часть этого равенства есть площадь Q поверхности, полученной от вращения кривой AB , в левой же части равенства обозначает длину окружности, описанной центром тяжести кривой при вращении её около оси x , а S есть длина нашей кривой. Таким образом, приходим к следующей теореме Гульдина:

Величина поверхности, полученной от вращения кривой около некоторой не пересекающей её оси, равна длине дуги этой кривой, умноженной на длину окружности, описанной центром тяжести C кривой (чертёж 12).