Курсовая работа: Проектирование и исследование кривошипно-ползунного механизма грохота

где l – расстояние на чертеже полного оборота кривошипа ОА, мм;

n – число оборотов в минуту вращения кривошипа ОА, об/мин, определяемое по формуле

(4.4)

Приняв длину полного оборота на чертеже 180 мм определим масштабы

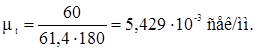
Масштаб перемещений возьмем несколько мельче

m_s =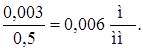

Графическое дифференцирование диаграмм скоростей и ускорений выходного звена. Выбрав произвольно полюсное расстояние H_v = (40…60 мм) = 50мм, вычислим масштаб диаграммы скоростей m_V

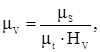(4.5)

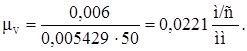
Заменяем кривую перемещения совокупностью хорд, выбираем полюсное расстояние и строим систему координат. Для этого на графике скоростей параллельно хордам строим прямые, проходящие через полюс. Из точки пересечения прямой с осью S проводим прямую, параллельную оси t до искомого положения. Полученные точки последовательно соединяем, получив в итоге график скоростей выходного звена. Аналогично диаграмме скоростей, выбрав произвольно величину полюсного расстояния H_А , равное 40 мм, вычислим масштаб диаграммы ускорений m_А

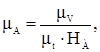(4.6)

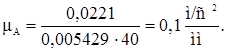
Построение диаграммы ускорений аналогично построению диаграммы скоростей.

Построение планов скоростей для трех положений

Для построения нужно знать скорость точки А во вращающем движении звена ОА. Определим ее из формулы:

V_{A 1} = (4.7)

V_{A 1} =

Для построения планов скоростей выберем положения механизма: первое, седьмое и десятое. Для всех положений построение аналогичное, поэтому опишем алгоритм построения. Определим характерные точки для построения: опорные – А1, В6, Д6, С3; и базовые – А3, Д4. Составим векторные уравнения скоростей этих точек:

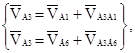(4.8)

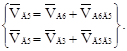(4.9)

Строим план скоростей. Кривошип ОА движется с постоянной скоростью. Из полюса – П плана скоростей в направлении вращения кривошипа перпендикулярно ОА откладываем вектор скорости (Па₁ ), условно приняв его длину равной 80 мм. После чего определяем масштаб плана скоростей:

m_V = 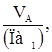(4.10)

m_V =

В соответствии с системой уравнений (4.8) делаем соответствующие построения. Для этого через точку а₁ проведем прямую, параллельную ВА, а из полюса П проведем прямую перпендикулярную АВ, так как скорость В6 равна нулю. Таким образом, получаем точку а₃ . Поскольку точка С принадлежит звену АВС, то на плане скоростей ее можно найти, использую теорему подобия. Определяем ее местоположение по соотношению длин рычага АВС и соотношений длин скоростей а₃ в₆ с₃ . Затем, используем систему векторных уравнений (4.9). Найдя точку с₃ , откладываем от нее перпендикуляр к шатуну СД. Из полюса проводим параллельную прямой ВД прямую; поскольку скорость точки b₆ равна нулю, то тем самым получим точку d₄ . Положения векторов скоростей центров масс определим из теоремы подобия. Поскольку центр масс звена ОА находится в точке О, то на плане скоростей он будет находиться в точке П. Положение центра S₄ на плане скоростей определим на линии с₃ d₄ , посередине отрезка. На отрезке b₆ а₃ найдем из пропорции (4.11) положение точки S₃ :

(4.11)