Курсовая работа: Проектирование механического привода с цилиндрическим соосным редуктором

ω_FV = 0,16 ^. 5,6 ^. 1,404 ^. = 11,32 Н/мм;

К_FV = 1 + = 1,225.

K_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий,

K_Fβ = ; (4.40)

где:

N_F = 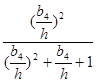; (4.41)

где: h – для прямозубого зацепления:

h = ; (4.42)

h = = 4,025;

N_F = 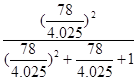= 0,949;

K_Fβ = = 1,095;

K_Fα = K_{н α} = 1 – коэффициент, учитывающий распределение нагрузки между зубьями:

К_F = 1,1 ^. 1,225 ^. 1,095 ^. 1 = 1,476;

Y_{FS 3} , Y_{FS 4} – коэффициенты, учитывающие форму зуба и концентрацию напряжений, определяемые для шестерни и колеса в зависимости от числа зубьев Z₃ и Z₄ по графику зависимости (рис. 4.2).

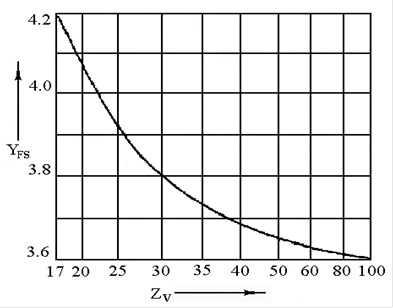
рис. 4.2

Y_β = 1 – коэффициент, учитывающий наклон зуба прямозубых передач;

Y_ε = 1 – коэффициент, учитывающий перекрытие зубьев:

Найдя все необходимые коэффициенты, найдём расчётное местное напряжение при изгибе для шестерни и колеса, МПа:

для шестерни:

σ_{F 3} = = 72,78 МПа;

для колеса:

σ_{F 4} = 72,78 ^. = 69,51 МПа.

Допускаемое напряжение, МПа:

σ_FP = ; (4.43)

где: σ_Flimb – предел выносливости зубьев при изгибе, МПа:

σ_Flimb = ; (4.44)

где: σ⁰ _Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа:

σ⁰ _Flimb = 1,75 ^. НВ; (4.45)