Курсовая работа: Проектирование системы оптимального корректирующего устройства
Проверим достаточное условие устойчивости. Для системы четвертого порядка достаточно проверить выполнение условия:
,
,
.
Условие выполняется, следовательно, система устойчива.
Проверим устойчивость системы по критерию Найквиста [1, §6.5, §6.6].
1. С использованием амплитудно-фазовой частотной характеристики (АФЧХ):
Запишем ПФ РС:
.
Для того чтобы судить об устойчивости замкнутой системы, необходимо проверить устойчивость разомкнутой системы. Для этого запишем характеристическое уравнение разомкнутой системы (ХУ РЗ) и найдем корни уравнения:
,
; 
; 
; 
.
Так как один из корней равен нулю (), а все остальные корни с отрицательными вещественными частями (левые), то можно сделать вывод, что разомкнутая система находится на апериодической границе устойчивости.
Далее необходимо построить АФЧХ разомкнутой системы (годограф Найквиста). Запишем выражение для построения АФЧХ и выделим действительную и мнимую части:
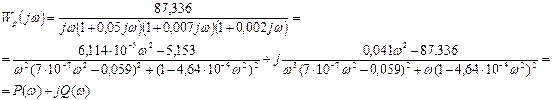
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Найквиста (рис. 1.8) по характерным точкам (табл. 1.4):
Таблица 1.4
|
ω |
|
|
|
0 |
-5,146 |
-∞ |
|
46,7 |
-0,7 |
0 |
|
290,3 |
0 |
0,008 |
|
К-во Просмотров: 615
Бесплатно скачать Курсовая работа: Проектирование системы оптимального корректирующего устройства
|
