Курсовая работа: Проектирование системы оптимального корректирующего устройства
0
0
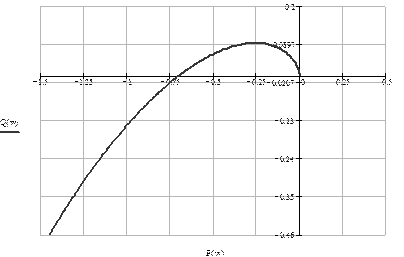
Рис. 1.8. Годограф Найквиста
Так как годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывает особую точку (−1;j0), то замкнутая система устойчива.
2. С использованием ЛЧХ:
Запишем выражения и построим ЛАЧХ и ЛФЧХ (рис. 1.9):
.
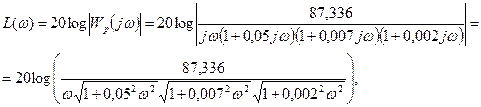
Рис. 1.9. ЛЧХ системы
Замкнутая система устойчива, если выполняется неравенство:
,
где 
– частота среза, при которой 
;
– критическая частота, при которой 
.
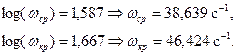
Так как неравенство 
выполняется, следовательно, замкнутая система устойчива.
Проверим устойчивость системы по критерию Михайлова [1, §6.3].
Запишем ХУ ЗС:
,
,
,
.
Подставим в этот полином чисто мнимое значение 
. При этом получим функцию Михайлова, как характеристический полином, состоящий из вещественной и мнимой части:
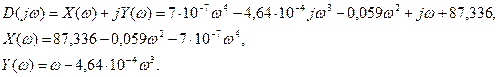
Задаваясь различными значениями ω в пределах от нуля до бесконечности, построим годограф Михайлова (рис. 1.10) по характерным точкам (табл. 1.5):
Таблица 1.5
|
|
|
К-во Просмотров: 617
Бесплатно скачать Курсовая работа: Проектирование системы оптимального корректирующего устройства
|
