Курсовая работа: Расчет информационных характеристик источников сообщений сигналов и кодов

В данной курсовой работе проводится расчет основных информационных характеристик источника сообщений, сигналов и каналов. Теория информации представляет собой ветвь статистической теории связи. Информация передается, и хранится в виде сообщений. Сообщение - это информация представленная в какой-либо форме. Первый раздел курсовой работы носит название: «Расчёт информационных характеристик источника дискретного сообщения». Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом . Сигнал передаётся по каналу связи. Второй раздел работы называется: «Расчёт информационных характеристик дискретного канала». В оставшихся двух разделах решаются задачи по темам: согласование дискретного источника с дискретным каналом с шумом и без шума, эффективное и помехоустойчивое кодирование. Их решение основываются на постулатах таких ученых как Шеннон, Хаффман, Фано.

1. Расчет информационных характеристик источников дискретных сообщений

1.1 Задача № 1.30

Распределение вероятностей дискретной случайной величины имеет вид:

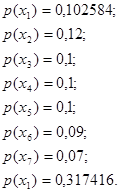
Определить число n значений случайной величины, при которых энтропия H_p (X) равномерного распределения будет равна энтропии H(X) заданного распределения.

Решение :

Определим энтропию заданного распределения. Для нахождении энтропии данного дискретного ансамбля воспользуемся формулой (1.4), соответствующей определению энтропии (Энтропия – это среднее количество информации, содержащееся в одном сообщение источника). Вычислим энтропию распределения:

.

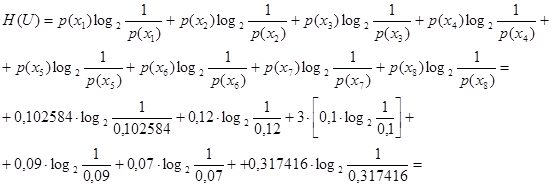
Равномерное распределение предполагает равные вероятности всех возможных исходов, при этом энтропия

.

Из условия, что

находим:

Ответ: при объеме алфавита n = 7 , энтропия H_p (X) равномерного распределения будет равна энтропии H(X) заданного распределения.

1.2 Задача № 1.48

Найти энтропию шума H(U/Z) в двоичном симметричном канале без памяти, если энтропия источника на входе канала H(U) = 3400(бит) , энтропия ансамбля на выходе канала H(Z) = 6800(бит) , ненадежность канала H(U/Z) = 700(бит) .

Решение:

Энтропия шума в двоичном симметричном канале без памяти будем искать по формуле

.

Выразим, неизвестное нам, количество информации

.

Подставляя эту формулу в исходную, получим выражение для нахождения энтропии шума в двоичном симметричном канале

.

Ответ : энтропия шума в двоичном симметричном канале H(U/Z) = 4100(бит) .

1.3 Задача № 1.67