Курсовая работа: Расчет информационных характеристик источников сообщений сигналов и кодов

Закодировать произвольную комбинацию, состоящую из пяти символов ансамбля А; Определить потенциальный минимум среднего количества символов кода, приходящихся на одно сообщение ансамбля А; Определить среднее количество символов разработанного кода Хаффмана, приходящихся на одно сообщение из ансамбля А; Рассчитать эффективность разработанного кода.

Решение :

Для удобства закодирования расположим вероятности появления сообщений в порядке убывания. Четыре последние вероятности объединяем в одну вспомогательную букву, которой приписывается суммарная вероятность. Вероятности, не учитывающиеся в объединении, и суммарная вероятность снова расположим в порядке убывания. Полученный ряд вероятностей записываем в таблицу и четыре последние вновь объединяем. Процесс будем повторять до последней вспомогательной буквы, с вероятностью, равной единице.

А3	0,503	0,503	0,503	1
А9	0,124	0,124	0,251
А2	0,122	0,122	0,124
A1	0,082	0,082	0,122
А4	0,04	0,0555
А11	0,0395	0,04
А8	0,034	0,0395
А12	0,0305	0,034
А5	0,012
А10	0,006
А7	0,005
А6	0,002

Затем строится кодовое дерево, в процессе которого осуществляется кодирование: верхняя точка дерева равна единице; из нее направляется четыре ветви, причем, ветви с большей вероятностью приписывается значение «4», а с меньшей – «0». Такое последовательное ветвление продолжается до тех пор, пока не добираются вероятности каждой буквы.

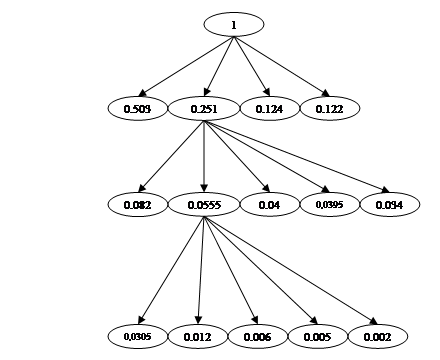
Рис.3.2

Затем, двигаясь по кодовому дереву сверху вниз, записываем для каждой буквы соответствующую ей кодовую комбинацию:

P1 = 0,82	24	n1 = 2
P2 = 0,122	0	n2 = 1
P3 = 0,503	3	n3 = 1
P4 = 0,004	22	n4 = 2
P5 = 0,012	233	n5 = 3
P6 = 0,002	230	n6 = 3
P7 = 0,005	231	n7 = 3
P8 = 0,034	20	n8 = 2
P9 = 0,124	1	n9 = 1
P10 = 0,006	232	n10 = 3
P11 = 0,0395	21	n11 = 2
P12 = 0,0305	234	n12 = 3

Выберем из ансамбля А произвольную комбинацию из пяти символов и закодируем их полученным кодом Хаффмана:

А₈ А₇ А₆ А₅ А₄

2023023023322.

Потенциальный минимум будем искать по формуле (2.12) лекции:

;

Так как код является четверичным, тогда основание кода N =5 . Следовательно:

.

Найдем энтропию источника, пользуясь мерой Шеннона:

;

Тогда потенциальный минимум

.

Рассчитаем среднее количество символов, приходящихся на одно сообщение:

, где

М – объем алфавита кода (М = 5 );

P_i – вероятность появления события;

n – количество символов в коде.

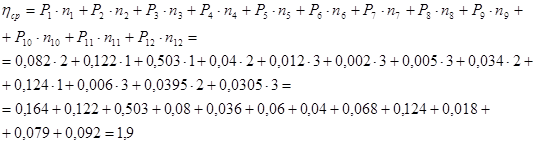
Согласно (2.12.а) лекции эффективность кода находим, как:

.

Ответ : потенциальный минимум ; среднее количество символов, приходящихся на одно сообщение ; эффективность кода .

4. Согласование дискретного источника с дискретным каналом с шумом. Помехоустойчивое кодирование

4.1 Задача № 4.24