Курсовая работа: Расчет информационных характеристик источников сообщений сигналов и кодов

Решение :

В соответствии с (1.12) лекции, избыточность источника дискретного сообщения с объемом алфавита М называется величина

,

Причем, если ввести понятие производительности

,

То величину можно переписать в виде:

.

Так как передача информации предполагает, что безошибочное кодирование должно быть однозначным, т.е. потери информации при кодировании должны отсутствовать. Это значит, что производительность канала должна быть равна производительности источника сообщения, т.е.

.

В соответствии с условием (2.15) теоремы Шеннона

или для оптимального кода

, где .

Поэтому, окончательная формула для вычисления избыточности будет выглядеть:

.

В соответствии с §1.6 лекции, среднее количество символов, передающихся в единицу времени будем определять по формуле (1.27.а):

Подставляя полученное значение в выведенную формулу избыточности, получим:

Ответ : минимальная возможнаяизбыточность оптимального кода для симметричного канала с вероятностью ошибки Р = 0,1 и объемом алфавита М = 3 будет равна .

4.2 Задача № 4.54

Построить производящую матрицу G линейного двоичного блочного кода, способного исправлять одиночную ошибку при передаче дискретных сообщений источника, представляющих собой последовательность десятичных цифр из диапазона 0 … M-1 (с объёмом алфавита M = 1981 ). Пользуясь разработанной матрицей G , сформировать кодовую комбинацию для сообщения i (i = 1569 ). Построить соответствующую производящей матрице G проверочную матрицу H и с её помощью сформировать кодовую комбинацию для сообщения i . По виду синдрома найти и исправить ошибку в принимаемой кодовой комбинации (дополнительно заданной преподавателем). Определить, является ли разработанный код кодом Хэмминга.

Решение :

Производящая матрица G линейного двоичного блочного кода имеет размерность (n; k ). Так как код является двоичным, то

.

Отсюда находим k :

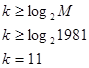
Матрица G линейного двоичного кода состоит из двух матриц:

.