Курсовая работа: Расчет напряжений деформаций в изотропном теле по заданному тензору напряжений

Тензор напряжений в главных осях имеет вид:

.

1.3 Определение положения главных осей тензора напряжений

Положение главных осей тензора напряжений определяется матрицей направляющих косинусов:

(13)

Здесь первая строка матрицы представляет направляющие косинусы главной оси, по которой действует напряжение ; вторая строка - направляющие косинусы главной оси, по которой действует напряжение ; третья строка - направляющие косинусы главной оси, по которой действует напряжение . Все направляющие косинусы задаются в исходной (старой) системе координат, показанной на рис. 1

Направляющие косинусы главных осей находятся из системы уравнений:

(14)

при условии

(15)

Здесь - направляющие косинусы главной оси тензора напряжений, вдоль которой действует напряжение .

В теории упругости (1) доказывается, что определитель, составленный из коэффициентов при неизвестных () системы уравнений (13), равен нулю. Следовательно, три уравнения в (13) являются линейно зависимые: одно уравнение (любое) является следствием двух других. Поэтому для определения направляющих косинусов любой главной оси нужно одно из уравнений удалить (любое) и к двум оставшимся добавить уравнение (14). Решив полученную систему трех уравнений с тремя неизвестными, найдем направляющие косинусы , соответствующие главному напряжению . Положение оставшихся двух осей находят аналогично.

Нужно иметь в виду, что каждый из направляющих косинусов получается с двумя знаками. Знаки соответствуют повороту осей по часовой стрелке или против часовой стрелки. При этом главные оси занимают одно и то же положение, но направлены в противоположные стороны.

При определении положения главных осей нужно оставить одну систему знаков, конкретизировав при этом направления осей.

1.3.1 Вычисление направляющих косинусов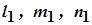

Для определения направляющих косинусов , соответствующих оси, вдоль которой действует напряжение , подставим в (14) и (15) ; при этом из (14) возьмем первые два уравнения (можно взять любые два):

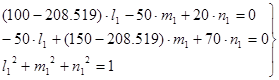(16)

Сначала найдем отношения между направляющими косинусами; для этого систему уравнений приведем к виду:

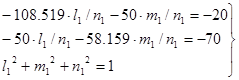(17)

Решая подсистему, состоящую из первых двух уравнений, получим:

. (18)

Подставляя эти выражения в третье уравнение (17), найдем:

, (19)

откуда

.

На этом этапе решения задачи можно у выбрать любой знак. Примем . Подставляя это значение в (18), получим:

. (20)

Углы, которые составляет первая главная ось тензора напряжений с исходными осями координат, находятся вычислением функции от :

.

Вычисление

Подставляя в (14) и (15) и используя те же два уравнения из (14) (можно и другие), получим: