Курсовая работа: Расчёт общей и местной вибрации корабля
4.16 Расчёт значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня для 5 вариантов значения длины корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
4.17 Расчёт значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня для 5 вариантов значения интенсивности веса "q" корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
4.18 Приведение результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня в сводной таблице
4.19 Сопоставление результатов расчётов. Выводы
5. Общая вибрация корабля. Расчёт параметров общей вибрации судового корпуса
5.1. Исходные данные
5.2 Определение частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика
5.3 Определение частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика-Бюрилля
5.4 Определение значений высших частот (второго, третьего и четвёртого тонов) свободных поперечных колебаний судового корпуса по формуле Центрального научно-исследовательского института имени академика А.Н. Крылова
5.5 Расчёт значений высших частот (второго, третьего и четвёртого тонов) свободных поперечных колебаний судового корпуса по рекомендациям Н.Н. Бабаева и В.Г. Лентякова
5.6 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика для 5 вариантов значения длины корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
5.7 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика для 5 вариантов значения интенсивности веса "q" корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
5.8 Приведение результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля по формуле Шлика в сводной таблице
5.9 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика-Бюрилля для 5 вариантов значения длины корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
5.10 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика-Бюрилля для 5 вариантов значения интенсивности веса "q" корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
5.11 Приведение результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля по формуле Шлика-Бюрилля в сводной таблице
5.12 Сопоставление результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля по формулам Шлика и Шлика-Бюрилля
5.13 Сопоставление результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня со значениями, определёнными по формулам Шлика и Шлика-Бюрилля
Литература
1. Силы, вызывающие вибрацию корпуса судна
1.1 Виды нагрузок, вызывающие вибрацию корпуса судна и его отдельных конструкций
Все нагрузки, вызывающие вибрацию корпуса корабля и его отдельных конструкций, целесообразно разделить на четыре вида.
К первому виду отнесем меняющиеся во времени силы, которые появляются вследствие неточностей, допущенных при изготовлении и монтаже судовых механизмов, валопроводов, гребных винтов.
Ко второму виду принадлежат нагрузки, связанные с тем, что гребные винты корабля работают за корпусом и в непосредственной близости от него.
Третий вид нагрузок составляют силы, вызванные воздействием на судно морского волнения.
Наконец, к четвертому виду будем относить различные динамические нагрузки, появляющиеся в специфических условиях эксплуатации судна: при взрывах, ударах о лед, ударах при швартовке и столкновениях и т.п.
1.2 Нагрузки, вызванные неточностями изготовления механизмов, валопроводов, винтов
Одним из основных дефектов, приводящих к появлению вибрационной нагрузки, следует считать неполную сбалансированность вращающихся или движущихся поступательно масс, которая может наблюдаться у главных и вспомогательных двигателей, редукторов, гребных валов и винтов.
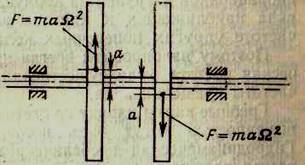
При статической неуравновешенности центр тяжести вращающейся части не лежит на оси вращения. Пусть а - отстояние центра тяжести от оси вращения, т - масса, Ω - угловая скорость.
Тогда на ротор действует радиальная (вращающаяся) сила:
F = таΩ2, которая передается на подшипники и фундамент механизма в виде периодической нагрузки.