Курсовая работа: Расчёт общей и местной вибрации корабля

"q"

кгс/cм

Модуль упругости

материала

"Е"

МПа

Момент инерции поперечного сечения

"I"

см⁴

8.2 0.22 210000 6200

2.3 Дифференциальное уравнение свободных колебаний упругой системы

Учитывая даламберовы силы, дифференциальное уравнение свободных колебаний однопролётной балки имеет вид:

(2.1)

2.4 Общее решение колебаний упругой системы

(2.2)

2.5 Дифференциальное уравнение для форм главных свободных колебаний призматического стержня

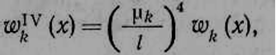(2.3)

где

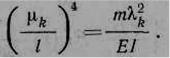(2.4)

2.6 Общий интеграл дифференциального уравнения для форм главных свободных колебаний

(2.5)

2.7 Граничные условия на свободно опёртых концах балки

Граничные условия для рассматриваемого стержня имеют вид:

Внося сюда выражение (2.2), получаем граничные условия для форм свободных колебаний:

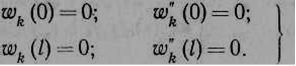(2.6)

2.8 Составление уравнений из условий подчинения граничным условиям на левом и правом концах балки

Подчиняя выражение (2.5) граничным условиям (2.6) функции w_k (х ) при х = 0 и х = L получаем систему линейных однородных алгебраических уравнений относительно неизвестных постоянных A_k , B_k , C_k и D_{/ e} :

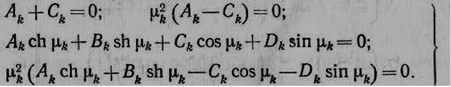(2.7)

2.9 Система линейных однородных алгебраических уравнений относительно неизвестных постоянных интегрирования

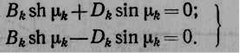(2.8)

2.10 Определитель системы. Уравнение частот

Интересующее нас решение, отличное от нуля, получаем при равенстве нулю определителя упомянутой выше системы уравнений (2.8):

Уравнение это называется уравнением частот.

(2.9)

откуда уравнение частот будет иметь вид: