Курсовая работа: Расчёт общей и местной вибрации корабля

Отсюда уравнение частот примет следующий вид:

sinμ_к = 0

Корни этого уравнения частот будут определяться по формуле:

μ_k = πk,

где k=l, 2, 3,...

2.11 Формулы для определения частот свободных колебаний

По найденным из уравнения частот корням μ _k ( k = 1, 2, 3,. .) с помощью формулы (2.4) определяются частоты свободных колебаний стержня:

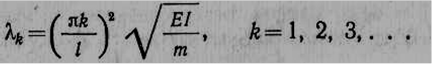(2.11)

Заметим, что обычно корни μ _k , ,а, следовательно, и частоты λ _k , нумеруются в порядке их возрастания:

2.12 Расчет значения частот первых пяти тонов свободных колебаний свободно опертого призматического стержня

Расчёт значения частот первых пяти тонов свободных колебаний свободно опёртого призматического стержня начинается с вычисления значения интенсивности массы самого призматического стержня, а именно:

,

тогда частоты первых пяти тонов свободных колебаний (2.11) будут равны:

при k = 1:

,

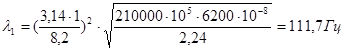при k = 2:

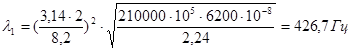
при k = 3:

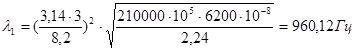
при k = 4:

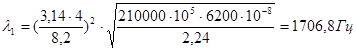
при k = 5:

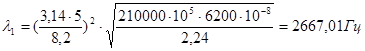
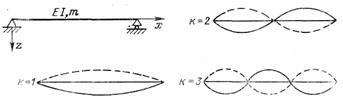
2.13 Выражение для определения форм свободных колебаний свободно опёртого призматического стержня

Из уравнений системы (2.8), если учесть результат sinμ_к = 0 , следует, что:

В_к = 0.

Таким образом, лишь постоянная D_k оказалась не равной нулю. Тогда на основании формулы (2.5), если подставить в нее найденные выше значения A_{k ,} B_k и C_{k ,} получим выражение для форм колебаний свободно опертой балки:

(2.12)

Таким образом, форма колебаний может быть определена с точностью до постоянного множителя, значение которого обычно выбирается исходя из удобства вычислений.

2.14 Расчёт и построение форм первых пяти тонов главных свободных колебаний свободно опёртого призматического стержня