Курсовая работа: Расчёт параметров изгиба прямоугольных пластин судового корпуса

Курсовая работа

"Расчёт параметров изгиба прямоугольных пластин судового корпуса"

Содержание

Прямоугольная пластина. Основные обозначения. Расчётная схема

Исходные данные

Цилиндрическая жесткость пластины

Заключение. Основные выводы

Список литературы

Прямоугольная пластина. Основные обозначения. Расчётная схема

Рассмотрим пластину постоянной толщины h , опертую на жесткий прямоугольный контур, у которого один в плане значительно больше другого (рис.1).

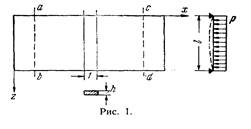
Пусть эта пластина загружена равномерно распределенной нагрузкой, величина которой, приходящаяся на единицу площади, есть р (Мы ограничиваемся рассмотрением случая, когда р = const, хотя излагаемая ниже теория справедлива и при р = р (z)). Очевидно, что такая пластина в своей средней части, ограниченной сечениями аb и сd, будет изгибаться по цилиндрической поверхности. Иными словами, пластина в средней части не будет иметь кривизны в плоскости хоу .

В связи с этим изгиб рассматриваемой пластины будет характеризоваться изгибом любой балки-полоски, мысленно выделенной из пластины, как показано на рис.1.

Пластинами называются упругие тела, имеющие форму призмы, расстояние между основаниями которой мало по сравнению с размерами оснований.

Геометрическое место точек, равноудаленных от оснований, образует срединную поверхность пластины. Длина отрезка перпендикуляра, восставленного к срединной поверхности между основаниями, называется толщиной пластины.

При исследовании изгиба прямоугольных пластин будем пользоваться декартовой системой координат. Плоскость хоу совместим со срединной плоскостью пластины, а ось оz направим вниз.

Размеры пластин в направлении осей ох и оу обозначим буквами а и b соответственно, а толщину пластины - буквой h (рис.2).

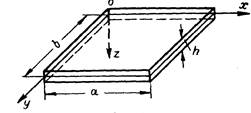
Рис.2

Исходные данные

№ п/п	Размер пластины (a), м	Размер пластины (b), м	Модуль упругости материала Е ·103 МПа	Толщина пластины (h), м
19	1.90	1,30	210	0.020

Дифференциальное уравнение изгиба абсолютно жестких пластин.

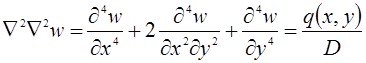(1)

Уравнение (1) представляет дифференциальное уравнение в частных производных с постоянными коэффициентами.

Интегрирование таких уравнений будем производить методом разделения переменных, используя для этой цели тригонометрические функции.

Выражения, устанавливающие связь между перемещениями пластины и значениями изгибающими моментами.

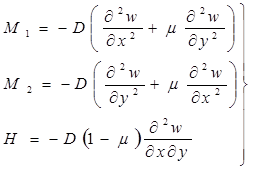(2)

где 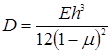- цилиндрическая жесткость пластины.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--