Курсовая работа: Расчет переходных процессов в электрических цепях. Формы и спектры сигналов при нелинейных преобразованиях
X(t) = Xпр (t) + Xсв (t).
Свободное решение Xсв (t) протекает в цепи без участия внешнего источника W(t), а принужденная составляющая Xпр (t) протекает в установившемся режиме под действием W(t). Свободная составляющая уравнения (1) находится в виде
Xсв (t) = Аеpt ,
где р =b0 /b1 является корнем характеристического уравнения
b1 p + b0 = 0,
Постоянная интегрирования А находится из начальных условий.
Переходные процессы в линейных цепях первого порядка
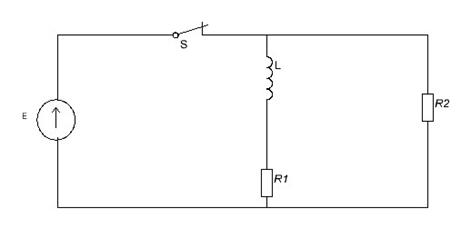
E= 70 В
R1 = 2 кОм
R2 = 3 кОм
L= 2 мГн
Определение независимой переменной.
IL– независимая переменная
Составляем дифференциальное уравнение для переходного процесса в электрической цепи и записываем его в общее решение
IL(t) = iсв (t) + iпр
Определяем начальные условия
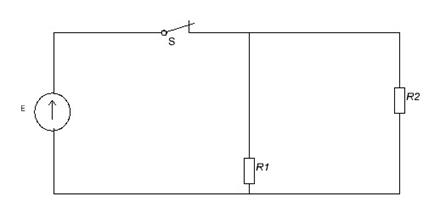
E=R1*iLiL = E/R1
iL = 70В/2 кОм = 35мА
Записываем решение дифференциального уравнения для свободной составляющей в виде
Iсв (t)= A*e p*t
![]()
![]()
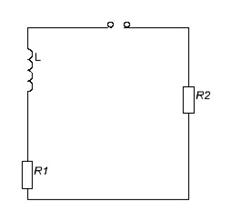
Zp = 0
p = -(R1+R2)/L p=-25*105
τ = 1/|p| τ = 4*10-7 (c)
Определяется принуждённая составляющая при t=∞
iпр=0