Курсовая работа: Расчет переходных процессов в электрических цепях. Формы и спектры сигналов при нелинейных преобразованиях
Запишем решение дифф. уравнения для свободной составляющей.
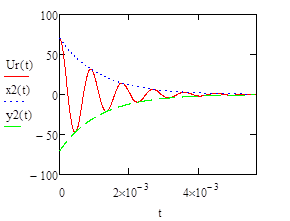
iсв (t)=A*eαt *sin(wt+θ)
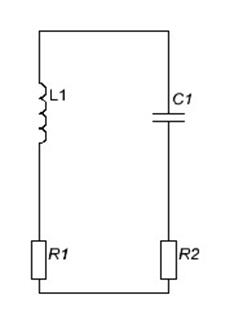
Zвх =2R+jwL+1/jwC
2R+pL+1/pC=0
LCp2 +2RCP+1=0
p=-883.833-7.016i*103
τ=1/|α|=1.131*10-3
T=2π/w=8.956*10-4
Определим принужденные составляющие при t=∞
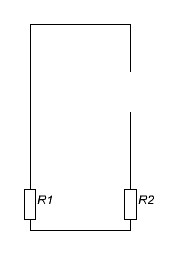
iпр =0
Определим постоянный интегрирования Aи θ
UL (t)=LAαweαt *sin(wt+θ)
iL (t)=Aeαt *sin(wt+θ)
LAα*sin θ+ LAw*cosθ =0
Asinθ=19.799
-Acos θ=2.494
tg θ=19.799/Acos θ=7.938
θ=1.455
A=19.955
 |
|
|
 |
 |
Спектральное представление периодических процессов в электрических цепях
Во многих случаях в установившемся режиме кривые периодических э.д.с., напряжений и токов в электрических цепях могут отличаться от синусоидальных. При этом непосредственное применение символического метода для расчета цепей переменного тока становится невозможным. Для линейных электрических цепей задача расчета может быть решена на основе метода суперпозиции с использованием спектрального разложения несинусоидальных напряжений и токов в ряд Фурье. В общем случае ряд Фурье содержит постоянную составляющую, первую гармонику, частота которой совпадает с частотой ω1 =2π/T периодического с периодом T тока или напряжения, и набор высших гармоник с частотами ωn =nω1 , кратными основной частоте ω1 . Для большинства периодических функций ряд Фурье содержит бесконечное число членов. На практике ограничиваются конечным числом членов ряда. При этом исходная периодическая функция будет представлена с помощью ряда Фурье с некоторой погрешностью.
Пусть имеется периодическая с периодом Т э.д.с. е(t)=e(t±nT), удовлетворяющая условиям Дирихле (функция на интервале Т имеет конечное число разрывов и экстремумов). Такая функция может быть представлена суммой гармонических составляющих с различными амплитудами Еn , частотами ωn =nω1 и начальными фазами φn в виде ряда Фурье
![]()
Ряд Фурье можно представить в другой форме:
![]()
Постоянная составляющая Е0 и коэффициенты ряда Фурье Вn и Сn рассчитываются по формулам