Курсовая работа: Расчет переходных процессов в электрических цепях. Формы и спектры сигналов при нелинейных преобразованиях
Определяется постоянная интегрирования А
IL (-0)= A*ept =A*e0*t =A
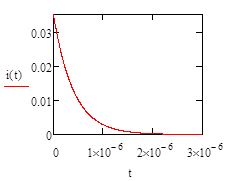
Ток через индуктивность равен:
IL (t)=35*10-3 * e-2500000 t
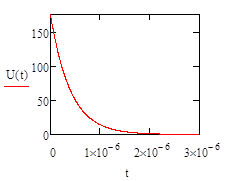
Напряжение на индуктивности равно:
UL (t)=-L (du/dt) = -AL*p*(E/R1) * ept
UL (t)=175 *e-2500000 t
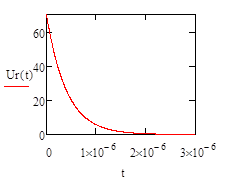
Напряжение на R1 равно:
UR1 (t)=70*e-2500000t
 |
 |
Переходные процессы в RLC цепях
Линейные цепи 2-го порядка содержат два разнотипных реактивных элемента L и C. Примерами таких цепей являются последовательный и параллельный резонансные контуры (рис.1).
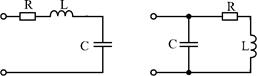
а б
Рис. 1. Линейные цепи второго порядка: а – последовательный резонансный контур; б – параллельный резонансный контур
Переходные процессы в колебательных контурах описываются дифференциальными уравнениями 2-го порядка. Рассмотрим случай разряда емкости на RL цепь (рис.2). Составим уравнение цепи по первому закону Кирхгофа:
![]() , (1)
, (1)
где
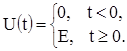
После дифференцирования (1) получим
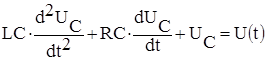 . (2)
. (2)
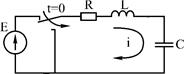 |
???. 2. ????????? RLC ???? ?? ?????????? ??????????
Решение Uс (t) уравнения (2) находим как сумму свободной Uсв (t) и принужденной Uпр составляющих
Uс =Uсв +Uпр . (3)
Uпр зависит от Е, а Uсв (t) определяется решением однородного дифференциального уравнения вида
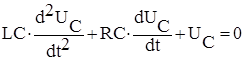 . (4)
. (4)
Характеристическое уравнение для (4) имеет вид
LCp² + RCp + 1 = 0, (5)
Корни характеристического уравнения
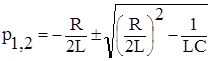 .
.