Статическая механическая характеристика привода при частотно-токовом управлении, в области скольжений меньше 1,5 S_ном описывается следующей зависимостью:

,

Где —жесткость механической характеристики. Определяется по формуле:

Видно, что механическая характеристика имеет линейный вид. Также для расчета необходимо найти максимальное значение момента с точки зрения нагрева. При этом учтем то, что машина является перегруженной:

М_max =М_ном **1,4=98,2*1,6=157 Н*м

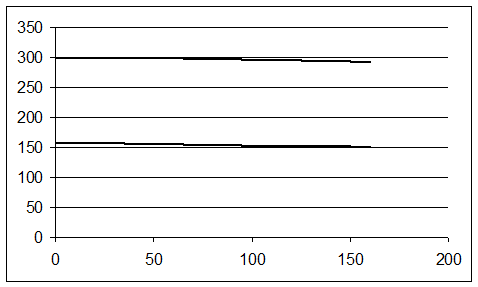
Рисунок 5.1—Механическая характеристика привода

Электромеханическая характеристика также будет линейна, т.к. при частотно-токовом управлении момент прямопропорционален току. Зависимость между моментом и током можно найти для номинальной точки.

А

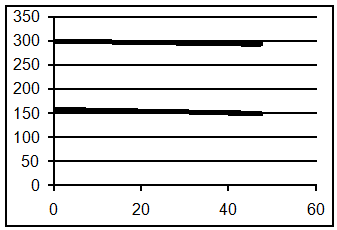
Рисунок 5.2—Электромеханическая характеристика.

6. Расчет переходных процессов в электроприводе за цикл работы

Для расчета регуляторов необходимо рассчитать коэффициенты передачи датчиков обратных связей. Будем считать, что датчики линейны и не входят в насыщение. Максимальное выходное напряжение датчика примем равным 10 В. Тогда коэффициент передачи рассчитывается как отношение максимального выходного напряжения к максимальному значению контролируемого параметра.

- К_дс =10/320=0,0313 В*с/рад;

- К_дн =10/2000=0,05 В/Н.

При синтезе упростим модель привода:

- Вследствие того, что момент инерции в процессе намотки изменяется в 16 раз, то для регулятора скорости момент инерции примем в 4 раза больше начального. Это повысит быстродействие при выборе провисания и выходе в режим с номинальным натяжением;

- Будем считать, что натяжение возникающее в ленте прямо пропорционально удлинению;

- Также будем считать, что радиус барабана не изменяется. Примем равным начальному значению. Это повысит быстродействие контура натяжения.

Расчет регулятора момента

Для получения наилучших динамических свойств, функциональный преобразователь должен быть реализован в силовом преобразователе.

Структурная схема контура момента с регулятором представлена на рисунке 6.1. Регулирование момента производим с помощью положительной обратной связи по скорости.

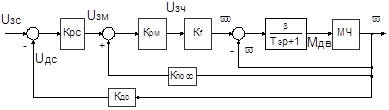
Рисунок 6.1—Контур момента

В статике:

М=(K_f *K_{Р M} *U_з +K_f *K_{Р M} *K_ПОСС *

Отсюда получается система уравнений: