Курсовая работа: Разработка и проектирование робота для разминирования

wC_j – ограничение по ускорению для j-го сочленения,

JC_j – ограничение по скорости изменения ускорения для j-го сочленения.

Q_ji (t) – кубический полином, описывающий поведение j-й присоединенной переменной между узловыми точками i и i+1, т.е. между H_i и H_{i +1} .

w_ji – ускорение в H_i ; оно соответствует Q_ji ’’(t_i ) если Q_ji (t) проходит через H_i в момент времени t_i .

X=(h₁ , h₂ ,…, h_{n -1} ),- вектор временных интервалов.

Задачу можно сформулировать следующим образом: минимизировать целевую функцию Т

при следующих ограничениях:

, j=1,2,…, N, i=1,2,…,n-1,

, j=1,2,…, N, i=1,2,…,n-1,

, j=1,2,…, N, i=1,2,…,n-1.

Строгое представление этих ограничений представлено ниже.

а) Ограничение по скорости.

, j=1,2,…, N, i=1,2,…,n-1,

Дифференцируя равенство (2) и заменяя Q_ji ’’(t_i ) и Q_ji ’’(t_{i +1} ) соответственно на w_ji и w_{j , i +1} , получаем:

Q_ji ’(t)=w_ji /2h_i *(t_{i +1} -t)² + w_{ji +1} /2h_i *(t-t_i )² + [q_{j , i +1} /h_i – h_i w_{j , i +1} /6] – [q_ji /h_i – h_i w_ji /6],

Также Q_ji ’’(t) можно представить как

Q_ji ’’(t)= w_j,i+1 /h_i *(t-t_i ) + w_ji /h_i *(t-t_i+1 ),

Скорость достигает своего максимального по абсолютной величине значения в одной из точек t_i , t_{i +1} или , где и Q_ji ’’()=0. Ограничение по скорости тогда принимает вид :

для i=1,2,…,n-1j=1,2,…,N, (6)

где

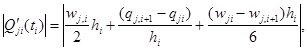
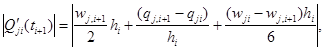
И

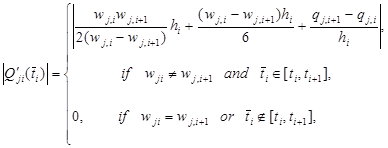
б) Ограничения по ускорению:

, j=1,2,…, N, i=1,2,…,n-1,

Между двумя узловыми точками ускорение линейно зависит от времени. Поэтому максимальная абсолютная величина ускорения достигается в точке t_i или в точке t_{i +1} и равна максимальной из величин .С учетом этого ограничение по ускорению принимает следующий вид: