Курсовая работа: Регулирующий клапан прямого действия

Если нельзя пренебречь инерцией подвижной системы клапана и силами трения, то условие равновесия сил, действующих на клапан, запишется как

_.

1. Определяем передаточную функцию элемента W(р).

Для этого воспользуемся исходным дифференциальным уравнением:

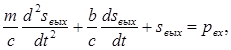
Учитывая, что постоянные времени и коэффициент передачи его равны:

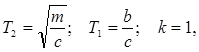
дифференциальное уравнение примет вид:

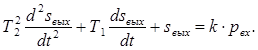(1)

Перейдем от дифференциального уравнения к операторной форме. Рассмотрим оператор дифференцирования: и подставим его в уравнение (1) получим.

Запишем передаточную функцию для нашего элемента:

Получили передаточную функцию регулирующего клапана.

2. Определяем частотную функцию элемента W(jω).

Пусть р – число мнимое, т. е. σ = 0, а р = jω, подставляем р в уравнение для передаточной функции, получим:

Где U (ω) = ReW(jω), а V (ω) = ImW(jω).

Также частотную форму передаточной функции можно представить в виде:

3. Определяем амплитудно-частотную функцию А (ω).

Построим график амплитудно-частотной функции А (ω):

4. Определяем фазо-частотную функцию φ (ω).

Построим график фазо-частотной функции φ (ω):

5. Определяем переходную функцию h (t).