Курсовая работа: Регулирующий клапан прямого действия

t_П ≈ (1÷2) 2π/ ω_ср ≈ (1÷2) 18,27 (с).

4. Полоса пропускания частот определяется:

Откладываем получившееся значение от A_max .

Получаем полосу пропускания:

ω₁ = 0,2154 и ω₁ = 0,2682.

3. Исследуем систему с уравнением

на устойчивость.

Для этого перейдем от дифференциального уравнения к операторной форме.

- оператор дифференцирования, подставим его в данное уравнение.

Получаем характеристическое уравнение:

,

Находим корни квадратного уравнения:

р = -1/Т₁ = -1,163.

Получили устойчивое состояние, т. к. α_i < 0, т. е. все корни характеристического уравнения находятся в левой полуплоскости.

Проведем оценку качества системы.

а) Прямая оценка качества:

Находим передаточную функцию W(p):

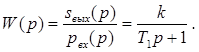
Запишем переходную функцию.

Построим график переходной функции h (t):

Так как система является устойчивой и график переходной функции не имеет колебаний, то можно определить только максимальное значение регулируемой величины, которое будет равно установившемуся:

h_мах = h_уст = 1.

Определим перерегулирование:

б) Косвенная оценка качества:

Рассмотрим амплитудно-частотную характеристику процесса.