Курсовая работа: Решение прикладных задач методом дихотомии

Введем обозначение

x₀

f()=f(x₀ )

Подставим в уравнение

Отсюда

x1=x₀ -

Шаг второй:

x2=x1-

Для n -го шага:

x_n =x_{n -1} -

Условием нахождения корня является:

2. Нелинейное уравнение и условие его решения:

, [1,2], ε = 0,0001;

3. График функции:

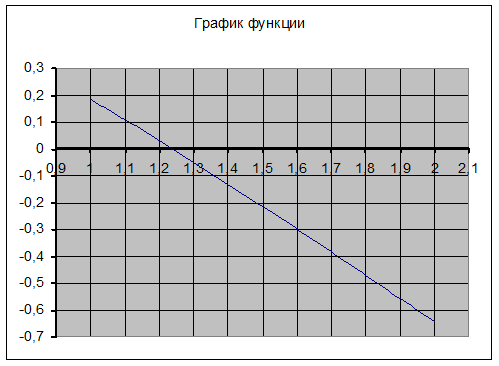
Таблица идетификаторов:

Обозначение	Идентификатор	Тип
n	n	int
	a	double
	b	double
	eps	double
x	x	double
f(x)	f(x)	double

6. Листинг программы :

#include<stdio.h>

#include<math.h>

double f(double x)

{

return (0.25*(pow(x,3)))+x-1.2502;

}

int main(void)

{

int n=0;

double x,a=1.,b=2.,eps=0.0001,xn;

xn=a;