Курсовая работа: Решение прикладных задач методом дихотомии

{

x=xn;

n++;

xn=x-f(x)*(b-x)/(f(b)-f(x));

printf("step=%3i x=%11.8lf f(x)=%11.8lf\n",n,xn,f(xn));

}

printf("pribligennoe znathenie x=%lf pri Eps=%lf\nkolithestvo iterasii n=%i\n",xn,eps,n);

return 0;

}

7. Листинг решения:

step= 1 x= 1.22334934 f(x)= 0.01236182

step= 2 x= 1.23796144 f(x)= 0.00070219

step= 3 x= 1.23879055 f(x)= 0.00003951

step= 4 x= 1.23883720 f(x)= 0.00000222

pribligennoe znathenie x=1.238837 pri Eps=0.0001

kolithestvo iterasii n=4

Анализ результатов:

метод дихотомии	метод хорд
значение корня	1.23889160	1.23883720
значение функции	-0.00004127	0.00000222
количество итераций	13	4

Вывод: Метод дихотомии прост в реализации, но обладает малой скоростью сходимости по сравнению с методом хорд, что выражается в количестве шагов. Метод хорд к тому же обладает большей точностью.

Часть 2

Решение дифференциального уравнения.

Вариант №11.

Метод Эйлера

1.Математическое описание

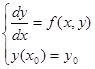
Геометрический смысл метода Эйлера состоит в следующем: дифференциальное уравнение определяет в точке (x₀ ,y₀ ) направление касательной к искомой интегральной кривой

k ₀ = y '( x ₀ )= f ( x ₀ , y ₀ )

Отрезок интегральной кривой, соответствующий x ( x ₀ , x ₁ ) , x ₁ = x ₀ + h заменяется участком касательной с угловым коэффициентом k . Найденная точка ( x ₁ , y ₁ ) используется в качестве нового начального условия для уравнения y ( x ₁ )= y _{1 ,} в ней вновь вычисляется угловой коэффициент поля направлений и процедура повторяется.

На n-ом шаге имеем точку (x_{n -1} ,y_{n -1} ), задающую начальное условие для уравнения:

y ( x_{n -1} )= y_{n -1}