Курсовая работа: Решение прикладных задач методом дихотомии

Соответствующее уравнение касательной:y - y_{n -1} = k ( x - x_{n -1} )

Отсюда получаем значение х=х_n , соответствующее точке: х _n =х _{n -1} + h ,

А именно: y_n - y_{n -1} = k_{n -1} ( x_{n -1} + h - x_{n -1} ), или

y_n =y_n-1 +h·k_n-1

y_n =y_n-1 +h·f(x_n-1, y_n-1 )

Полученная формула является основной расчетной формулой метода Эйлера.

Процесс вычислений заканчивается, когда аргумент после очередного приращения выйдет за пределы исследуемого отрезка .

2. Дифференциальное уравнение:

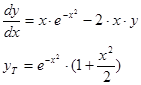x₀ = 0 , y₀ = 1, x_max =1, Δx = 0.01; 0.005; 0.001

3. Схема алгоритма:

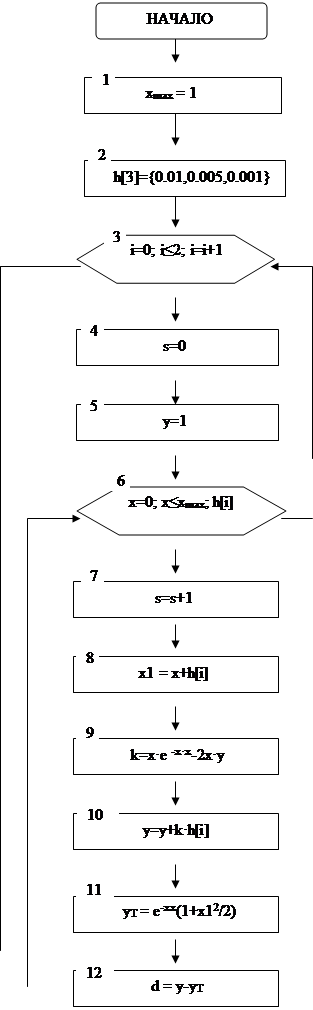5. Таблица идентификаторов:

Обозначение	Идентификатор	Тип
s	s	int
i	i	int
x	x	double
xmax	x_max	double
x1	x1	double
Δx	h[i]	double
y	y	double
d	d	double
f(x)	f(x)	double
k	k(x,y)	double

6. Листинг программы:

#include<stdio.h>

#include<math.h>

double k(double x,double y )

{

return ((x/exp(x*x))-2.*x*y);

}

double f(double x)

{

return ((1./exp(x*x))*(1+x*x/2.));

}

int main(void)

{

int s,i;

double x,x1,x_max=1,y,d;

double h[3]={0.01,0.005,0.001};

FILE*file;