Курсовая работа: Режим переконденсации с компактным распределением размеров капель

Классические работы Дж.Гиббса, М.Фольмера, Ф.Беккера, В.Дёринга, Я.Френкеля, Я.Зельдовича по физике фазовых переходов I рода относятся к ранним стадиям зарождения новой фазы.

В данной же работе нас интересует процесс конденсации, переходящий из флуктуационного режима роста зародышей новой фазы в стадию переконденсации, именуемую также коалесценцией, или Оствальдовским созреванием [ [i] ], когда рост крупных капель происходит за счёт растворения более мелких (при условии, что все капли далеки друг от друга).

Режим переконденсации может проходить в одном случае под управлением поглощающей способности поверхности (теория Вагнера: [ [ii] ]), когда длина свободного пробега молекулы много больше радиуса капли , а в другом случае под управлением диффузии в паре (теория Лифшица-Слёзова: [ [iii] , [iv] ]), когда .

Причиной расхождения эксперимента с теорией Лифшица-Слёзова-Вагнера оказалось допущение неограниченного объёма кластеров новой фазы [ [v] ].

Поэтому все дальнейшие теоретические исследования Оствальдовского созревания предполагают компактное основание распределения капель по размерам [ [vi] , [vii] , [viii] ].

Поэтому задачей данной работы является описание уравнений и параметров режима переконденсации в условиях существования максимального размера капли.

Коалесценция имеет большое практическое значение, например, в образовании и стабильности поверхностей [ [ix] , [x] , [xi] ].

Оглавление

Описание проблемы и постановка задачи. 1

Оглавление . 2

1). Переписывание уравнений в терминах максимальной капли. 3

2). Соотношения интегральных моментов функции распределения. 5

3). Нахождение автомодельной функции распределения. 6

4). Нормировка функции распределения. 9

5). Предельный случай – распределение Лифшица-Слёзова. 10

6). Графики. 11

7). Литература. 12

8) Ссылки . 12

1). Переписывание уравнений в терминах максимальной капли.

Оригинальные уравнения теории переконденсации записываются в терминах отношения безразмерного радиуса капли к её критическому радиусу в зависимости от безразмерного времени: . Наша задача – переписать их в терминах отношения радиуса капли к максимальному радиусу: .

Уравнение роста радиуса капли в режиме коалесценции Лифшица-Слёзова:

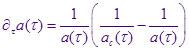
Тогда уравнение непрерывности для функции распределения по размерам капель:

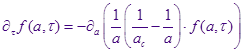
Подставляем сюда асимптотический анзац Лифшица-Слёзова в новых переменных и с явной зависимостью от времени:

Преобразуем дифференциальное уравнение (обозначая ):

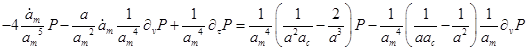
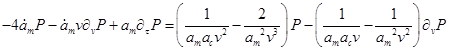
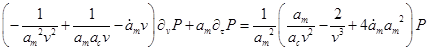
--> ЧИТАТЬ ПОЛНОСТЬЮ <--