Курсовая работа: Режим переконденсации с компактным распределением размеров капель

Удовлетворяя условию нормировки, подставим из . При сохранится только первый член:

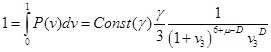
Так что функция распределения в нормированном виде равна:

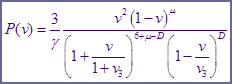
Из самого ( / ) дифференциального уравнения легко выписать производную функции распределения:

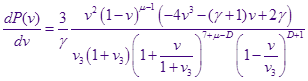
Приравняв её нулю и решая каноническое кубическое уравнение по формуле Кардано, имеем для максимума функции распределения, изменяющего своё положение с изменением :

5). Предельный случай – распределение Лифшица-Слёзова.

Рассмотрим предельный случай при . При этом из , а из . Тогда как их разность , что было показано в . Нам также пригодится асимптотика:

Приведём для сравнения функцию Лифшица-Слёзова, записанную в оригинальных переменных :

6). Графики.

Здесь нарисованы функции распределения из , охватывающие весь интервал возможных вплоть до функции Лифшица-Слёзова .

Литература.

1. А.Н.Васильев, А.К.Казанский, Л.Ц.Аджемян: « Переконденсация пересыщенного пара: аналитические теории и численный эксперимент ».

2. П.Губанов, Ю.Желтов, И.Максимов, В.Морозов: « Кинетический кроссовер режимов коалесценции в пересыщенном однородном растворе ».

3. В.Бойко, Х.Могель, В.Сысоев, А.Чалый « Особенности метастабильных состояний при фазовых переходах жидкость-пар »

4. В.Ф.Разумов: « Курс лекций по синергетике ».

5. Е.М.Лифшиц, Л.П.Питаевский: « Физическая кинетика ».

6. B.Giron, B.Meerson, P.V.Sasorov: « Weak selection and stability of localized distributions in Ostwald ripening ».

7. V.M.Burlakov: « Ostwald Ripening on nanoscale ».