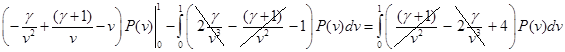Курсовая работа: Режим переконденсации с компактным распределением размеров капель
Приравнивание коэффициентов при 
(находим 
):
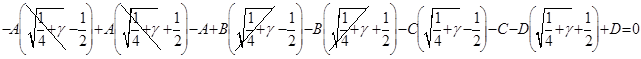
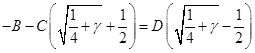
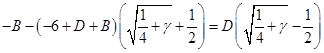
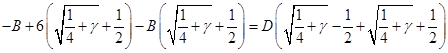
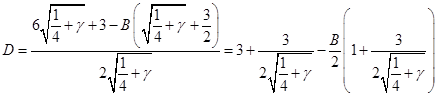
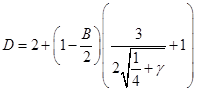
Подставляя полученное выражение для 
, выразим 
только через 
и избавимся от иррациональности в знаменателе:
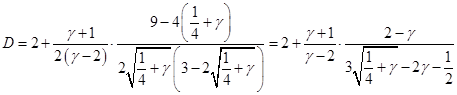
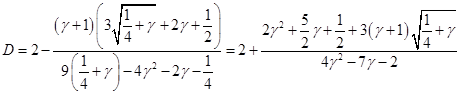
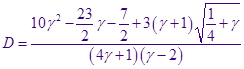
Таким образом, найдены все коэффициенты в разложении на простые дроби подынтегрального выражения в , интегрируя их, получаем, помня об области определения переменных:
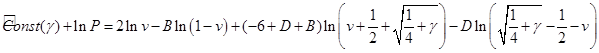
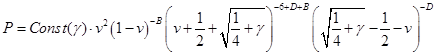
В значениях 
(третий корень 
) из окончательно запишем:
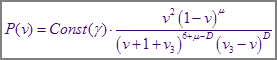
Где в силу физической ограниченности функции распределения на конце интервала, полагаем:
Оценим выражение для 
из :
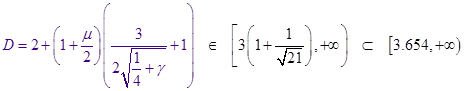
Дифференцированием и грубой оценкой можно увидеть, что 
монотонно убывает по
из бесконечности, как и 
. При этом величина 
, фигурирующая в , остаётся ограниченной (не имеет особенности при 
), более того почти постоянной в заданном интервале , в чём можно убедиться, вычитая в форме из 
и выражая всё через :
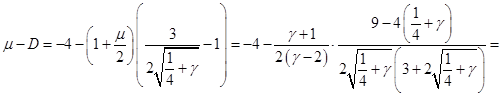
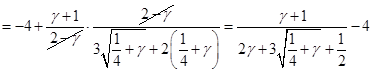
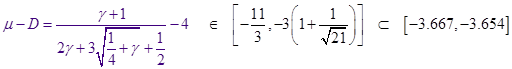
4). Нормировка функции распределения.
Как в пункте 2 проинтегрируем от 0 до 1 левую и правую части (без члена с производной по времени), предварительно разделив их на 
:
Формально интегрируем по частям левую часть:
