Курсовая работа: Режим переконденсации с компактным распределением размеров капель
![]()
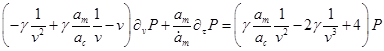
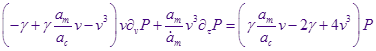
Избавимся от ![]() , подставив
, подставив ![]() в уравнение роста радиуса капли :
в уравнение роста радиуса капли :
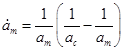
![]()
![]()
С учётом этого, а также определения ![]() в , докажем, что
в , докажем, что ![]() является корнем кубического полинома:
является корнем кубического полинома:
![]()
![]()

Тогда окончательно запишется следующим уравнением на функцию распределения:

Зная один корень, найдём делением по схеме Горнера квадратичное выражение в ![]()
|
корень 1 |
| ||||
|
-1 |
0 |
|
| ||
|
| остаток | ||||
|
-1 |
|
|
|
остаток = нулю
Таким образом:
![]()
Решим квадратное уравнение, полагая корни существующими:
![]()