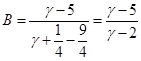Курсовая работа: Режим переконденсации с компактным распределением размеров капель

Каждая скобка в таком виде разложения, как мы увидим далее, будет положительна. Заметим также, что (так что), что, впрочем, сразу следует из теоремы Виета для по отсутствию квадратичного члена.

Итак, уравнение запишется следующим образом:

В этой работе мы рассмотрим автомодельную функцию , не зависящую явно от времени, при этом в полученном дифференциальном уравнении опускается член с частной производной по времени от функции распределения.

2). Соотношения интегральных моментов функции распределения.

Соотношения между интегральными моментами функции распределения можно найти, не зная её явного вида. Для этого проинтегрируем от 0 до 1 левую и правую части дифференциального уравнения , опуская член с производной по времени и вводя моменты:

Интегрируем по частям левую часть:

Это выражение, в сущности, означает, что , а если вспомнить отношение между максимальным и критическим радиусами капли, то получим равенство среднего и критического радиусов:

, когда функция распределения нормирована на единицу (см. РїСѓРЅРєС‚ 4 )

3). Нахождение автомодельной функции распределения.

По-прежнему полагая автомодельным и убирая в член с производной по времени, можно явно решить дифференциальное уравнение интегрированием:

Для этого разложим подынтегральное выражение на простейшие дроби и найдём коэффициенты:

При :

При :