Курсовая работа: Рішення ірраціональних рівнянь

Відповідь: {6}.

Приклад 2. Вирішити рівняння .

Рішення. У лівій частині вихідного рівняння коштує арифметичний квадратний корінь - він по визначенню ненегативний, а в правій частині - негативне число.

Отже, рівняння не має кореня.

Відповідь: .

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду.

, якщо й не має рішення, якщо .

Приклад 3. Вирішити рівняння .

Рішення. Зведемо обидві частини вихідного рівняння в куб.

; .

Відповідь: {-5}.

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду: .

2.2 Рівняння виду

Досить часто при рішенні рівнянь даного виду учні використовують наступне формулювання властивості добутку «Добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю». Помітимо, що формулювання властивості добутку повинна виглядати в такий спосіб: « добуток двох співмножників дорівнює нулю, коли хоча б один з них дорівнює нулю, а іншої при цьому має сенс».

Запишемо рівносиль, за допомогою якої вирішуються рівняння даного виду:

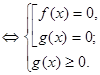
Приклад 1. Вирішити рівняння .

Рішення.

.

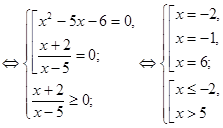Відповідь: {-2;6}.

Приклад 2. Вирішити рівняння .

Рішення. У цьому випадку рівняння не має виду, зазначеного в заголовку. Отже, його необхідно перетворити. Але спочатку знайдемо ОПЗ змінної .

ОПЗ: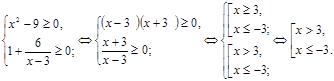

Перетворимо рівняння до виду

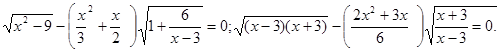
При рішенні рівняння учні часто необґрунтовано ділять обидві частини рівняння на вираження, що містить невідоме (у цьому випадку, на ), що приводить до втрати кореня й придбанню «стороннього». Подібні рівняння, що містять в обох частинах загальний множник, варто вирішувати переносом всіх членів в одну частину й розкладанням отриманого вираження на множники.

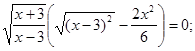
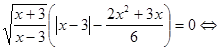
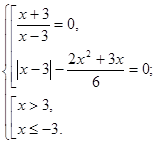
Вирішимо кожне рівняння із сукупності.

; .