Курсовая работа: Рішення ірраціональних рівнянь

Рішенням системи є множина:

.

Вирішимо рівняння системи.

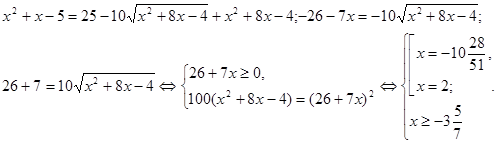
Переконуємося, що 2 належить множині рішень нерівності (мал.1).

Зауваження. Якщо вирішувати дане рівняння введенням обох частин у квадрат, то необхідно виконати перевірку. 2 - ціле число, тому при виконанні перевірки труднощів не виникають. А що стосується значення , то підстановка його у вихідне рівняння приводить до досить складних обчислень. Однак такої підстановки можна уникнути, якщо помітити, що при цьому значенні права частина рівняння приймає негативне значення: . Тоді як ліва частина рівняння негативної бути не може. Таким чином, не є коренем рівняння - наслідку даного рівняння. Тим більше, це значення не може бути коренем вихідного рівняння. Отже, корінь рівняння - число 2.

Приклад 6. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: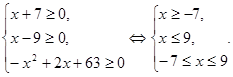

Отже,

Для будь-яких значень із ОПЗ, що задовольняють умові , тобто для із проміжку ліва частина рівняння негативна, а перша – ненегативна, виходить, жодне із цих рішенням рівняння бути не може.

Нехай . Для таких обидві частини рівняння ненегативні, і тому воно рівносильне на цій множині рівнянню:

.

Уведемо нову змінну. . Одержуємо, що . Тоді - не задовольняє умові , .

Виконаємо зворотну заміну.

; ;

.

Тоді - не задовольняє умові ,

Відповідь: .

Приклад 7. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ:

Отже, що

Легко бачити, що , тому що .

Розділимо обидві частини рівняння на . Одержуємо, що

Перетворимо . Уведемо нову змінну. Нехай , а . Тоді рівняння прийме вид: ; ; : . Тоді

«

1

2

3

4

5

6

7

8

»

• >>> Скачать <<<