Курсовая работа: Рішення ірраціональних рівнянь

. ,

те рівняння (6) є наслідком вихідного рівняння. Тоді, складаючи рівняння (5) і (6), одержимо рівняння (7), що також є наслідком вихідного рівняння (5). Зведемо обидві частини рівняння (6) у квадрат, одержимо рівняння (8), що також є наслідком вихідного рівняння. Вирішуючи рівняння (8), одержуємо, що ,

Перевіркою переконуємося, що обоє цих числа є коріннями вихідного рівняння.

Відповідь: .

Зауваження. Рівняння виду можна вирішувати множенням обох частин рівняння на деяке вираження, що не приймає значення нуль (на сполучене лівій частині рівняння тобто

Приклад 2. Вирішити рівняння (8).

Рішення. , те помножимо обидві частини рівняння на вираження , що є сполученим лівої частини рівняння (8). . Після приведення подібних доданків одержуємо рівняння (9), рівносильне вихідному, тому що рівняння дійсних корінь не має. Складаючи рівняння (8) і (9) одержуємо, що . Тоді

Відповідь: .

Зауваження. Також рівняння виду можна вирішувати за допомогою ОПЗ рівняння й рівносильних переходів від одних рівнянь до інших.

Приклад 3. Вирішити рівняння

Рішення. Знайдемо ОПЗ змінної х.

ОПЗ: Отже,

На ОПЗ обидві частини рівняння позитивні, тому після введення у квадрат одержимо рівняння: , рівносильне для рівнянню

Іноді рішення рівняння можна знайти, вирішуючи його на різних числових проміжках.

Для кожного маємо , а . Отже, серед немає рішень рівняння .

Для маємо . Отже, для . . Тоді . Так як , те є коренем рівняння , рівносильному рівнянню для цих х.

Відповідь: .

Приклад 4. Вирішити рівняння

Рішення. Перетворимо вихідне рівняння.

Зведемо обидві частини даного рівняння у квадрат.

Перевірка показує, що 5 є коренем вихідного рівняння.

Зауваження. Іноді значно простіше можна вирішувати рівняння виду , якщо скористатися властивостями монотонності функцій, а саме тим, що сума двох зростаючих функцій є зростаючою функцією, і всяка монотонна функція кожне своє значення приймає, лише при одному значенні аргументу. Дійсно, функції й - зростаючі. Отже, їхня сума - зростаюча функція.

Виходить, вихідне рівняння, якщо має корінь, те тільки один. У цьому випадку, з огляду на, що , підбором легко знайти, що 5 є коренем вихідного рівняння.

Приклад 5. Вирішити рівняння

Рішення. Якщо обидві частини вихідного рівняння піднести до квадрата, то вийде досить складне рівняння. Надійдемо по-іншому: перетворимо рівняння до виду:

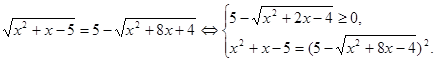
Вирішимо нерівність системи.