Курсовая работа: Рівносильні та рівновеликі багатокутники

(рис. 3.8) , переконуємося , що площа незаштрихованої частини паралелограма дорівнює площі заштрихованої, а площа всього паралелограма дорівнює .

Задача 3.

Паралелограми й у яких сторони й лежать на одній прямій , рівновеликі ( рис.3.9).

Рішення

Трапеція є , з одного боку, об'єднання трикутника й паралелограма ( рис.3.10) , з іншого боку, об'єднання трикутника й паралелограма ; трикутники й рівні.

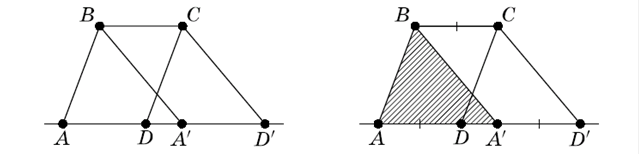
Рис.3.9 Рис.3.10

Задача 4.

Дано паралелограм . Розглянемо новий параллеограмм , у якого одна вершина збігається з вершиною , сусідня з нею вершина лежить на стороні , а сторона протилежна стороні , лежить на прямій , що проходить через вершину ( рис.3.11). Доведіть, що паралелограми й рівновеликі.

Рішення

Можна вважати (див. попередню задачу) , що сторона містить точку (рис.3.12). Трикутник - „загальний” для обох паралелограмів ,

по задачі 1.

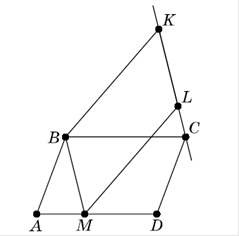
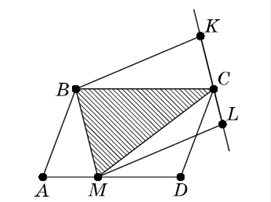
Рис.3.11 Рис.3.12

Задача 5.

Медіана трикутника ділить його на два рівновеликих трикутники.

Рішення

Нехай - медіана трикутника . Добудуємо трикутник до паралелограма , провівши через точку пряму , паралельну , а через точки й – прямі , параллелтные ( рис. 3.13). Паралелограми й рівні : паралельний перенос на вектор переводить перший з них у другий . Тому .

Діагональ паралелограма ділить його на два рівних трикутники, виходить,

і

Отже,

Рис.3.13

Задача 6.

Медіани трикутника ділять його на 6 рівновеликих частин.

Рішення

Нехай - точка перетинання медіан і трикутника ( рис.3.14) . – медіана трикутника , виходить, ; позначимо цю величину через . Нехай також . Оскільки – медіана трикутника , ,тобто , звідки . Аналогічно