Курсовая работа: Рух механічної системи із двома ступенями волі

(2.5)

Тепер проектуємо диференціальне рівняння (2.2) на координатну вісь :

(2.6)

При підстановці відомих значень одержимо:

(2.7)

Приведемо (2.7) до наступного виду:

(2.8)

Тут – це власна частота. Для знаходження залежності вирішимо дане рівняння.

– рішення шуканого диференціального рівняння буде складатися із загального рішення відповідного однорідного рівняння й будь-якого приватного рішення .

Загальне рішення маєте вигляд: (2.9).

Знайдемо приватне рішення рівняння (2.8), воно буде мати вигляд: . Перша й друга похідні: , .

Підставляючи частка рішення і його похідні в (2.8), одержимо:

Знаходимо значення постійних коефіцієнтів: , .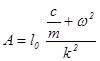

(2.10)

Тоді, виходячи з (2.9) і (2.10), рішення вихідного диференціального рівняння:

Для визначення констант інтегрування, використовуємо початкові умови:

, або ; звідки .

, або , звідки .

Підставивши значення й , і згрупувавши доданки, одержимо диференціальні рівняння відносного руху кульки і його швидкості:

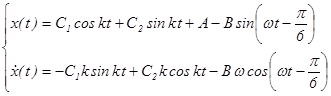(2.11)

Тут , , , , .

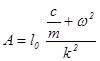3. Застосування загальних теорем динаміки до дослідження руху механічної системи

3.1 Складання рівняння руху твердого тіла за допомогою теореми про зміну кінетичного моменту

Механічною системою називається така сукупність матеріальних крапок, у якій положення й рух кожної крапки залежить від положення й руху інших крапок. Одержувані для системи матеріальних крапок теореми й співвідношення можна поширити й на системи, що складаються з одного або декількох взаємозалежних твердих тел. Обмеження, що накладаються на рух крапок і тіл механічної системи, називаються зв'язками. Виходячи із принципу свободи від зв'язків, рух кожної крапки системи можна розглядати як рух вільної крапки, якщо замінити дія зв'язків реакціями цих зв'язків. Тоді для кожної крапки, відповідно до основного рівняння динаміки матеріальної крапки, маємо:

(3.1.1)

і – маса й прискорення деякої крапки механічної системи; і – зовнішні й внутрішні сили (уже містять у собі реакції зв'язків).