Курсовая работа: Рух механічної системи із двома ступенями волі

Теорема про зміну кінетичного моменту формулюється в такий спосіб: повна похідна за часом від вектора кінетичного моменту механічної системи щодо деякого нерухливого центра по величині й напрямку дорівнює головному моменту зовнішніх сил, прикладених до механічної системи, певному щодо того ж центра:

(3.1.2)

Тут – кінетичний момент механічної системи щодо нерухливого центра ; він є мірою руху системи навколо цього центра й складається з кінетичних моментів всіх крапок і тіл, що входять у цю систему; – головний момент зовнішніх сил щодо нерухливого центра .

Визначимо головний момент зовнішніх сил:

, де й – плечі сил ваги кульки й трикутника;

(3.1.3)

Визначимо кінетичний момент системи. Він складається з кінетичних моментів кульки й трикутника: .

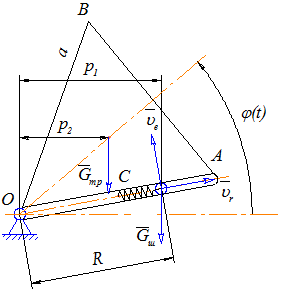
Малюнок 3.1.1. Складання рівняння руху твердого тіла за допомогою теореми про зміну кінетичного моменту

, де модуль переносної швидкості дорівнює .

(3.1.4)

, – момент інерції трикутника щодо шарніра . Визначимо його по теоремі Штейнера:

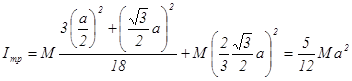(3.1.5)

(3.1.6)

З огляду на (3.1.4) і (3.1.6), кінетичний момент системи дорівнює:

(3.1.7)

Диференціюємо вираження (3.1.7):

(3.1.8)

Підставивши знайдені значення в (3.1.2), теорема про зміну кінетичного моменту прийме вид:

(3.1.9)

3.2 Визначення закону зміни зовнішнього моменту, що забезпечує сталість кутової швидкості

При дії зовнішнього моменту , що забезпечує рівномірне обертання механічної системи навколо шарніра , остання доданок у лівій частині рівності (3.1.9) звертається в нуль:

, ; звідси .

Тоді вираження (3.1.9) прийме вид:

(3.2.1)

спрямований протилежно головному моменту зовнішніх сил, тобто, проти годинникової стрілки.

Зовнішній момент, що забезпечує рівномірне обертання конструкції, дорівнює:

(3.2.2)

4. Визначення реакцій в опорах обертового тіла