Курсовая работа: Рух механічної системи із двома ступенями волі

(5.1.13) і (5.1.14) - це система рівнянь Лагранжа II роду; перше з них являє собою диференціальне рівняння відносного руху. При порівнянні (5.1.13) з рівнянням відносного руху (2.7) видно, що рівняння тотожні:

(2.7)

(5.1.13)

5.3 Визначення закону зміни зовнішнього моменту, що забезпечує сталість кутової швидкості

(5.1.14) - це рівняння рівняння руху твердого тіла без обмеження на закон зміни кутової швидкості обертання. Визначимо величину зовнішнього моменту, що забезпечує рівномірне обертання:

(5.1.14)

При дії зовнішнього моменту, що забезпечує рівномірне обертання, рівняння (5.1.14) прийме вид:

(5.3.1)

Звідси:

(5.2.2)

Зрівняємо з отриманим раніше значенням:

(3.2.2)

Отже, два різних способи визначення зовнішнього моменту дали один результат.

6. Визначення положень рівноваги механічної системи й дослідження їхньої стійкості

Важливим випадком руху механічних систем є їхній коливальний рух. Коливання - це повторювані рухи механічної системи щодо деякого її положення, що відбуваються більш-менш регулярно в часі. У курсовій роботі розглядається коливальний рух механічної системи щодо положення рівноваги (відносного або абсолютного).

Механічна система може робити коливання протягом досить тривалого проміжку часу тільки поблизу положення стійкої рівноваги. Тому перед тим, як скласти рівняння коливального руху, треба знайти положення рівноваги й досліджувати їхня стійкість.

Відповідно до основного рівняння статики, для того щоб механічна система перебувала в рівновазі, необхідно й досить, щоб у цій системі були дорівнюють нулю всі узагальнені сили:

(6.1)

– узагальнені сили; – число узагальнених координат у механічній системі.

У нашім випадку механічна система перебуває в потенційному силовому полі; з рівнянь (6.1) одержуємо наступні умови рівноваги:

(6.2)

Отже, у положенні рівноваги потенційна енергія має екстремальне значення. Не всяка рівновага, обумовлена вищенаведеними формулами, може бути реалізоване практично. Залежно від поводження системи при відхиленні від положення рівноваги говорять про стійкість або нестійкість даного положення. Достатні умови стійкості положень рівноваги для консервативних систем визначаються теоремою Лагранжа - Дирихле: «Положення рівноваги консервативної механічної системи стійко, якщо в ньому потенційна енергія системи має ізольований мінімум».

Визначимо положення рівноваги для заданої механічної системи, використовуючи раніше знайдені узагальнені сили (5.1.11) і (5.1.12) із системи рівнянь:

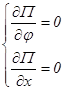
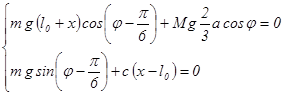(6.4)

Для нашої механічної системи маємо:

Перше положення рівноваги: , .

Друге положення рівноваги: , .

Використовуючи теорему Лагранжа - Дирихле визначаємо, що перше положення рівноваги є не стійким, а друге - стійким.