Курсовая работа: Сигналы и процессы в радиотехнике СиПРТ

. (3.13)

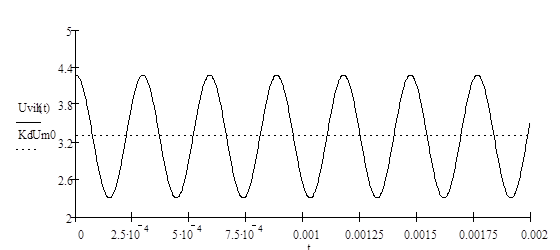
Рисунок 3.2 - График сигнала на выходе детектора.

Изобразим ВАХ диода, а также временные диаграммы тока диода и напряжения на диоде:

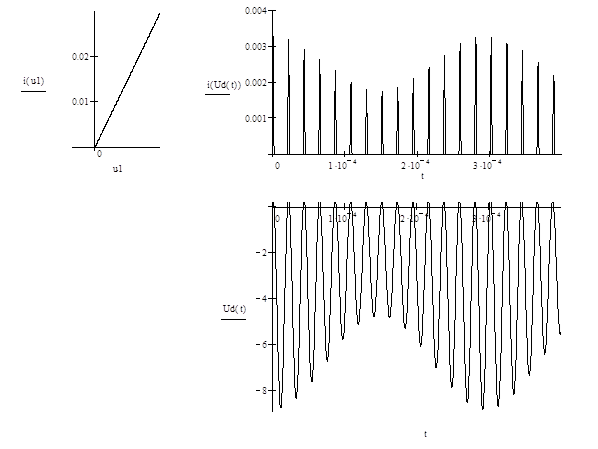Рисунок 3.3 – График ВАХ диода, временные диаграммы тока диода и напряжения на диоде

Задание №4

Генератор на полевом транзисторе с контуром в цепи стока генерирует гармоническое колебание с частотой . Контур состоит из индуктивности L , емкость C и имеет добротность Q . Крутизна сток-затворной характеристики транзистора в рабочей точке S .

Условие :

1. Изобразить электрическую схему генератора. Записать дифференциальное уравнение и вывести условие самовозбуждения генератора.

2. Определить критические коэффициенты включения .

3. Выбрать значение P , обеспечивающее устойчивую генерацию и рассчитать неизвестный элемент контура.

4. Изобразить качественно процесс установления колебаний в генераторе, указать области нестационарного и стационарного режимов.

Исходные данные :

Индуктивная трехточечная схема;

Решение:

1. Представим принципиальную схему индуктивного трехточечного автогенератора [2] :

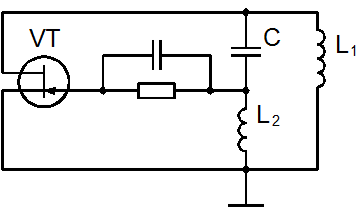
Рисунок 4.1 – Автогенератор, собранный по индуктивной трехточечной схеме.

Для составления дифференциального уравнения генератора рассмотрим колебательный контур подробнее, при этом как бы разорвав обратную связь (рисунок 4.2).

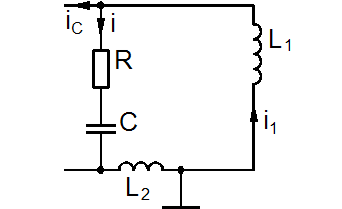
Рисунок 4.2 – Колебательный контур автогенератора.

В схеме на рисунке 4.2 R – сопротивление потерь контура.

По законам Кирхгофа и, используя компонентные уравнения элементов запишем систему характеристических уравнений [6] цепи представленной на рисунке 4.2.

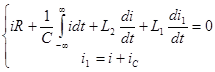. (4.1)

Для решения системы (4.1) не хватает еще одного уравнения. Его мы возьмем воспользовавшись характеристиками транзистора:

. (4.2)

Теперь проведя необходимые подстановки запишем уравнение с одним неизвестным током i .

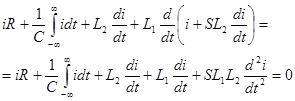. (4.3)

Чтобы избавиться от интеграла продифференцируем уравнение (4.3) по времени.

. (4.4)

Обозначим коэффициенты при неизвестном и его производных, как и соответственно при дифференциалах 0-ого, 1-ого, 2-ого и 3-его порядков. Тогда (4.4) примет вид:

. (4.5)

Для определения условия самовозбуждения воспользуемся критерием устойчивости Рауса-Гурвица [2] . В соответствии с этим критерием, для самовозбуждения необходимо и достаточно чтобы выполнялось:

1) 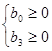; (4.6)

2) . (4.7)

Подставляя значения коэффициентов , получим условие самовозбуждения автогенератора.

. (4.8)

2. Определим критические коэффициенты включения индуктивности. Для этого проведем в (4.8) некоторые преобразования.

Поскольку индуктивность не отрицательна и не равна 0, то разделим (4.8) на нее.

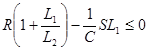. (4.9)