Курсовая работа: Сигналы и процессы в радиотехнике СиПРТ
Исходя из (4.10) и (4.11) можно записать:
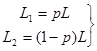. (4.12)
Подставим (4.12) в (4.9).
. (4.13)
Как известно 
- характеристическое сопротивление контура. Т.о. неравенство (4.13) примет вид:
. (4.14)
Разделив (4.14) на 
получим:
, (4.15)
но 
это есть добротность контура Q .
. (4.16)
Теперь если учесть, что 
(4.15), а затем умножить неравенство на 
, получим окончательное уравнение для вычисления критических коэффициентов включения.
. (4.17)
Используя [3] определим критический коэффициент включения индуктивности:
3. Рассчитаем неизвестный элемент контура (в нашем случае это индуктивность) по следующей формуле:
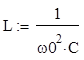(4.18)
Подставив исходные данные, получим:
Определим коэффициент усиления усилителя:
Найдём значения индуктивностей L1 и L2 при помощи [3] , используя операцию Given:
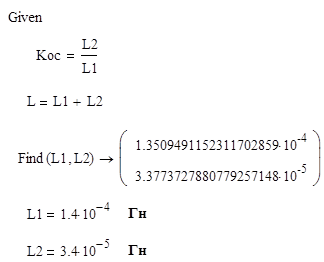
4. Представим качественный график процесса установления колебаний в автогенераторе (рисунок 4.3):
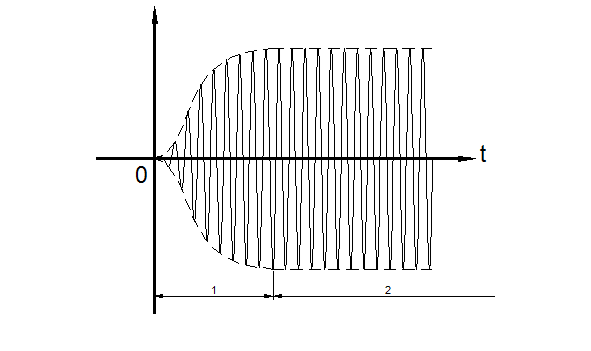Рисунок 4.3 – Процесс установления автоколебаний:
1. Нестационарный режим – режим, при котором параметры колебания меняются.
2. Стационарный режим – режим, при котором параметры колебания не меняются.
Задание №5.
Условие:
Аналоговый сигнал S ( t ) (рисунок 5.1) длительностью 
подвергнут дискретизации путем умножения на последовательность 
- импульсов. Интервал дискретизации Т .
Требуется:
1. Рассчитать спектр аналогового сигнала S ( t ) и построить график модуля спектральной плотности.
2. Определить максимальную частоту в спектре аналогового сигнала 
, ограничив спектр, использовав один из критериев.
3. Рассчитать интервал дискретизации Т и количество выборок N . Изобразить дискретный сигнал под аналоговым в том же временном масштабе.
4. Определить спектральную плотность дискретного сигнала и построить график модуля под графиком спектра аналогового сигнала и в том же частотном масштабе.
5. Провести дискретное преобразование Фурье (ДПФ), определить коэффициенты ДПФ и построить спектрограмму модуля этих коэффициентов под графиками спектров аналогового и дискретного сигналов и в том же частотном масштабе.
Записать выражение для Z - преобразования дискретного сигнала.
Решение: