Курсовая работа: Статистические методы выявления взаимосвязей общественных явлений

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции , который рассчитывается по одной из формул:

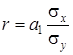(6.16)

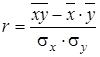. (6.17)

а также

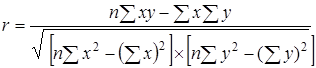или .

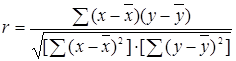Корреляционный анализ выполняет оценку адекватности регрессионной модели, но путем установления тесноты связи.

Оценка линейного коэффициента корреляции

Значение r	Характер связи	Интерпретация связи
r = 0	Отсутствует	Изменение x не влияет на изменения y
0 < r < 1	Прямая	С увеличением x увеличивается y
-1 > r > 0	Обратная	С увеличением x уменьшается y и наоборот
r = 1	Функциональная	Каждомузначениюфакторногопризнакастрогосоответствует одно значение результативного

Значимость линейного коэффициента корреляции проверяется на основе t- критерия Стьюдента. Для этого определяется фактическое значение критерия :

, (6.18)

Вычисленное по формуле (6.18) значение сравнивается с критическим , который получают по таблице Стьюдента с учетом принятого уровня значимости и числа степеней свободы ν.

Коэффициент корреляции считается статистически значимым, если t _расч превышает ( t _расч > ).

Универсальным показателем тесноты связи является теоретическое корреляционное отношение :

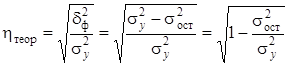, (6.19)

где – общая дисперсия эмпирических значений y , характеризует вариацию результативного признака за счет всех факторов, включая х ;

– факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у ;

– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х .

По правилу сложения дисперсий:

, т.е. 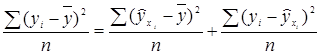. (6.19)

Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)

Значение	Характер связи	Значение	Характер связи
η = 0	Отсутствует	0,5 ≤ η < 0,7	Заметная
0 < η < 0,2	Очень слабая	0,7 ≤ η < 0,9	Сильная
0,2 ≤ η < 0,3	Слабая	0,9 ≤ η < 1	Весьма сильная
0,3 ≤ η < 0,5	Умеренная	η = 1	Функциональная

Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = |r| .

Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:

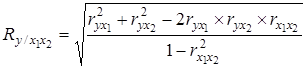, (6.20)

где – парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками.

Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:

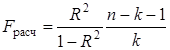, (6.21)

где R ² – коэффициент множественной детерминации (R ² );

k – число факторных признаков, включенных в уравнение регрессии.

Связь считается существенной, если F _расч > F _табл – табличного значения F- критерия для заданного уровня значимости α и числе степеней свободы ν₁ = k ,ν₂ = n – k – 1.