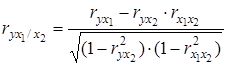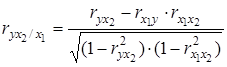; , (6.22)

где r – парные коэффициенты корреляции между указанными в индексе переменными.

В первом случае исключено влияние факторного признака х ₂ , во втором – х _1.

Для оценки сравнительной силы влияния факторов, по каждому фактору рассчитывают частные коэффициенты эластичности :

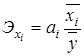, (6.23)

где – среднее значение соответствующего факторного признака;

– среднее значение результативного признака;

– коэффициент регрессии при i -м факторном признаке.

Данный коэффициент показывает, на сколько процентов следует ожидать изменения результативного показателя при изменении фактора на 1% и неизменном значении других факторов.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i -го признака, входящего в множественное уравнение регрессии, рассчитывается по формуле:

, (6.24)

где – парный коэффициент корреляции между результативным и i -м факторным признаком;

– соответствующий стандартизованный коэффициент уравнения множественной регрессии:

. (6.25)

Практическая часть

Выявить зависимость между нераспределенной прибылью и инвестициями в основные фонды, применяя:

А) метод параллельных рядов

Б) метод группировок

В) графический метод

3.2. Измерить тесноту связи между указанными признаками

Таблица№1

Для изучения капитальных вложений в производство из собственных средств предприятий в регионе проведена 5%-я механическая выборка, в результате которой получены следующие данные:

№ п/п	Нераспределенная прибыль, млн. руб.	Инвестиции в основные фонды, млн.руб.
А	1	2
1	2,2	0,06
2	2,0	0,04
3	4,3	0,44
4	5,0	0,6
5	6,0	0,90
6	2,3	0,12
7	3,6	0,20
8	4,2	0,36
9	5,8	0,80
10	4,7	0,60
11	2,5	0,18
12	3,8	0,40
13	4,5	0,53
14	4,8	0,65
15	4,4	0,42
16	5,4	0,70
17	5,2	0,50
18	4,1	0,35
19	3,3	0,20
20	5,6	0,70
21	3,9	0,40
22	4,8	0,73
23	4,5	0,62
24	4,7	0,70
25	3,4	0,30

1. Метод параллельных рядов. Произведем ранжирование капитальных вложений в производство по нераспределенной прибыли

Таблица№2

№ п/п	Нераспределенная прибыль, млн. руб.	Инвестиции в основные фонды, млн.руб.
А	1	2
1	2	0,04
2	2,2	0,06
3	2,3	0,12
4	2,5	0,18
5	3,3	0,2
6	3,4	0,3
7	3,6	0,2
8	3,8	0,4
9	3,9	0,4
10	4,1	0,35
11	4,2	0,36
12	4,3	0,44
13	4,4	0,42
14	4,5	0,53
15	4,5	0,62
16	4,7	0,6
17	4,7	0,7
18	4,8	0,65
19	4,8	0,73
20	5	0,6
21	5,2	0,5
22	5,4	0,7
23	5,6	0,7
24	5,8	0,8
25	6	0,9

После проведения ранжирования четко видна взаимосвязь нераспределенной прибыли от инвестиций в основные фонды. При большей прибыли инвестиции в основные фонды больше.

2. Метод группировок. Для образования групп предприятий по нераспределенной прибыли необходимо определить величину интервала по формуле Стерджесса:

I = x max - x min

n , где

х мах - наибольший показатель нераспределенной прибыли в млн. руб.

х min – наименьший показатель нераспределенной прибыли в млн. руб.