Курсовая работа: Статистический анализ выборочных совокупностей

1) ;

2) ;

3) .

Центральный момент третьего порядка случайной величины Х характеризует асимметрию (скошенность) распределения и служит для вычисления коэффициента асимметрии , который определяется по формуле

. (7)

Асимметрия положительна, если «длинная часть» кривой плотности распределения расположена справа от математического ожидания. Асимметрия отрицательна, если «длинная часть» кривой распределения расположена слева от математического ожидания.

Центральный момент четвертого порядка случайной величины Х характеризует «крутость» или островершинность графика ее плотности распределения и служит для вычисления эксцесса , который определяется по формуле

. (8)

Эксцесс положительный, если кривая распределения имеет острую вершину. Эксцесс отрицательный, если кривая распределения имеет пологую вершину.

Равномерное распределение вероятностей

Распределение вероятностей называют равномерным, если на интервале (a; b), которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:

(9)

Функция равномерного распределения на интервале (a; b) имеет вид:

Характеристики равномерного распределения определяются по формулам (2) – (4), (7), (8):

1) математическое ожидание ;

2) дисперсия ;

3) среднее квадратическое отклонение ;

4) асимметрия ;

5) эксцесс .

Вероятность попадания случайной величины Х, распределенной по равномерному закону, в заданный интервал (х₁ ; х₂ ) определяется по формуле (1)

.

Показательное распределение

Показательным (экспоненциальным) называют распределение непрерывной случайной величины Х, которое описывается плотностью

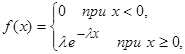(10)

где λ – постоянная положительная величина.

Функция показательного распределения имеет вид:

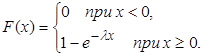
Характеристики показательного распределения определяются по формулам (2) – (4):