Курсовая работа: Статистический анализ выборочных совокупностей

2) дисперсия ;

3) среднее квадратическое отклонение .

Вероятность попадания случайной величины Х, распределенной по показательному закону, в заданный интервал (х₁ ; х₂ ) определяется по формуле (1)

. (11)

Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

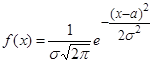(12)

Математическое ожидание нормального распределения равно параметру а. Среднее квадратическое отклонение нормального распределения равно параметру σ. Коэффициент асимметрии и эксцесс нормального распределения равны нулю: и .

Вероятность попадания нормально распределенной случайной величины Х в заданный интервал (х₁ ; х₂ ) определяется по формуле (1):

, (13)

где Ф(х) – функция Лапласа,

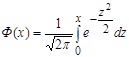. (14)

4. Статистический анализ выборочной совокупности

Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов. Объемом n выборочной совокупности называют число объектов этой совокупности.

Интервальным статистическим распределением выборки называют перечень интервалов и соответствующих им частот n_i или относительных частот .

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (плотность частоты).

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 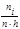(плотность относительной частоты).

Для распределения наблюдений по интервалам необходимо найти длину интервала h, определяемую как отношение разности между максимальным X_{ma х} и минимальным X_min элементами выборки к количеству интервалов k

. (15)

Количество интервалов k (целое число) целесообразно выбрать не менее 7, но и не более 15 или определить по формуле Старджесса

, (16)

где n – объем выборки.

Если k, вычисляемое по формуле Старджесса, нецелое число, то в качестве числа интервалов можно ближайшее к k целое число, не меньшее k.

Статистические оценки параметров распределения

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения х₁ , х₂ , …., х_n выборки объема n различны, то

.

Если значения признака х₁ , х₂ , …., х_k имеют соответственно частоты n₁ , n₂ , …..n_k , причем n₁ +n₂ +……+n_k =n, то

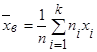. (17)

Для характеристики рассеяния значений количественного признака Х выборки вокруг своего среднего значения вводят такой параметр как выборочная дисперсия.

Выборочной дисперсиейD_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения х₁ , х₂ , …., х_n признака различны, то